题目内容
已知直棱柱的底面是边长为3的正三角形,高为2,则其外接球的表面积
| A.6仔 | B.8仔 | C.12仔 | D.16仔 |
D
解析考点:球的体积和表面积.
专题:计算题.
分析:根据直棱柱的底面边长及高,先得出棱柱底面外接圆的半径及球心距,进而求出三棱柱外接球的球半径,代入球的表面积公式即可得到棱柱的外接球的表面积.
解答:解:由正三棱柱的底面边长为3,
得底面所在平面截其外接球所成的圆O的半径r=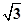 ,
,
又由正三棱柱的侧棱长为2
,则球心到圆O的球心距d=1,
根据球心距,截面圆半径,球半径构成直角三角形,
满足勾股定理,我们易得球半径R满足:
R2=r2+d2=4,R=2,
∴外接球的表面积S=4πR2=16π.
故答案为:D.
点评:本题考查的是棱柱的几何特征及球的体积和表面积,考查数形结合思想、化归与转化思想,其中根据已知求出三棱柱的外接球半径是解答本题的关键.

练习册系列答案
相关题目
有一个几何体的三视图及其尺寸如下(单位:cm),则该几何体的体积为:
A.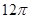 cm3 cm3 | B. cm3 cm3 | C. cm3 cm3 | D. cm3 cm3 |
如图,将装有水的长方体水槽固定底面一边后倾斜一个小角度 ,则倾斜后水槽中的水形成的几何体是
,则倾斜后水槽中的水形成的几何体是 ( )
( )
| A.棱柱 | B.棱台 | C.棱柱与棱锥 的组合体 的组合体 | D.不能确定 |
已知四棱锥 的三视图如下图所示,则四棱锥
的三视图如下图所示,则四棱锥 的体积为( )
的体积为( )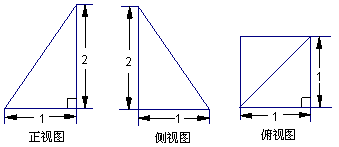
A. | B. | C. | D. |
一空间几何体的三视图如图2所示, 该几何体的体积为 ,则正视图中x的值为
,则正视图中x的值为
| A. 5 | B.4 | C.3 | D.2 |
若某空间几何体的三视图如图所示,则该几何体的体积是
| A.2 | B.1 | C. | D. |

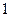




 B 1∶3 C 1∶3
B 1∶3 C 1∶3