题目内容
过抛物线的焦点F作互相垂直的两条直线,分别交准线于P、Q两点,又过P、Q分别作抛物线的对称轴OF的平行线,交抛物线于M、N两点,则M、N、F三点( )A.共圆
B.共线
C.在另一抛物线上
D.分布无规律
解析:设M(x1,y1)、N(x2,y2),抛物线方程为y2=2px,
则F(p2,0),准线x=-![]() .
.
∴P(-p2,y1),Q(-p2,y2).
由PF⊥QF,得![]() ·
·![]() =-1.
=-1.
∴y1y2=-p2,
k MF=![]() =
=![]() ,
,
k NF=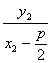 =
=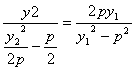
∴k MF=k NF.
∴M、N、F三点共线.
答案: B

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
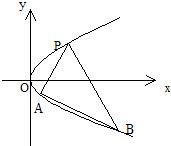 如图,过抛物线y2=2px(p>0)上一定点P(x0,y0)(y0>0),作两条直线分别交抛物线于A(x1,y1),B(x2,y2)
如图,过抛物线y2=2px(p>0)上一定点P(x0,y0)(y0>0),作两条直线分别交抛物线于A(x1,y1),B(x2,y2)
 的点到其焦点F的距离
的点到其焦点F的距离 的值,并证明直线AB的斜率是非零常数.
的值,并证明直线AB的斜率是非零常数.
 的点到其焦点F的距离
的点到其焦点F的距离 的值,并证明直线AB的斜率是非零常数.
的值,并证明直线AB的斜率是非零常数.
 的点到其焦点F的距离
的点到其焦点F的距离 的值,并证明直线AB的斜率是非零常数.
的值,并证明直线AB的斜率是非零常数.