题目内容
已知函数![]() 在区间
在区间![]() 上为增函数,且
上为增函数,且![]() 。
。
(1)当![]() 时,求
时,求![]() 的值;
的值;
(2)当![]() 最小时,
最小时,
①求![]() 的值;
的值;
②若![]() 是
是![]() 图象上的两点,且存在实数
图象上的两点,且存在实数 ![]() 使得
使得![]() ,证明:
,证明:![]() 。
。
解: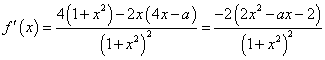 。…………2分
。…………2分
(1)当![]() 时,由
时,由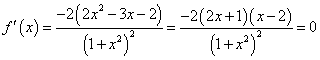 ,
,
得![]() 或
或![]() ,
,
所以![]() 在
在![]() 上为增函数,在
上为增函数,在![]() ,
,![]() 上为减函数,…………4分
上为减函数,…………4分
由题意知![]() ,且
,且![]() 。
。
因为![]() ,所以
,所以![]() ,
,
可知![]() 。 ………………7分
。 ………………7分
(2)① 因为![]() ,
,
当且仅当![]() 时等号成立。……8分
时等号成立。……8分
由![]() ,有
,有![]() ,得
,得![]() ;…………9分
;…………9分
由![]() ,有
,有![]() ,得
,得![]() ;…………10分
;…………10分
故![]() 取得最小值时,
取得最小值时,![]() ,
,![]() 。 …………11分
。 …………11分
②此时,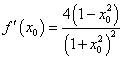 ,
,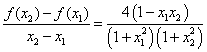 ,
,
由![]() 知,
知,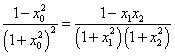 ,…………12分
,…………12分
欲证![]() ,先比较
,先比较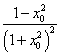 与
与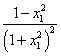 的大小。
的大小。

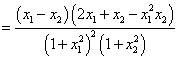
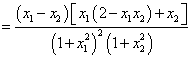
因为![]() ,所以
,所以![]() ,有
,有![]() ,
,
于是![]() ,即
,即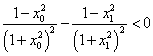 ,…………13分
,…………13分
另一方面,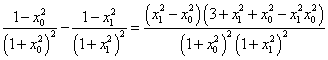 ,
,
因为![]() ,所以
,所以![]() ,从而
,从而![]() ,即
,即![]() 。…14分
。…14分
同理可证![]() ,因此
,因此![]() 。 …………15分
。 …………15分

练习册系列答案
相关题目
 在区间
在区间 上为增函数,且
上为增函数,且 。
。 时,求
时,求 的值;
的值; 最小时,
最小时, 的值;
的值; 是
是 图象上的两点,且存在实数
图象上的两点,且存在实数 使得
使得 ,证明:
,证明: 。
。  在区间
在区间 上为增函数,那么
上为增函数,那么 的取值范围是.
的取值范围是.
 在区间
在区间 上为增函数,且
上为增函数,且 。
。 时,求
时,求 的值;
的值; 最小时,
最小时, 的值;
的值; 是
是 图象上的两点,且存在实数
图象上的两点,且存在实数 使得
使得 ,证明:
,证明: 。
。