题目内容
在野外为测量河对面的一座建筑物的高,准备有皮尺(可量距离)、水平仪(可量水平角、倾斜角),测量工作在河另一岸平地上进行,请你设计两种不同的测量方案,画出示意图,并写出计算过程和结果.(所测距离用a,角用α,β,γ表示,水平仪高为h)
分析:方案一:水平仪高为h,测量者在点C测得点A的仰角为α,前进am,到达点D测得点A的仰角为β,则可求AB
方案二:水平仪高为h,测量者在点C测得点A的仰角为α,向另一方向,∠CBD=γ,前进am,到达点D测得点A的仰角为β,则可求AB
方案二:水平仪高为h,测量者在点C测得点A的仰角为α,向另一方向,∠CBD=γ,前进am,到达点D测得点A的仰角为β,则可求AB
解答:解:设建筑物的高为(AB+h)m
方案一:水平仪高为h,测量者在点C测得点A的仰角为α,前进am,到达点D测得点A的仰角为β,则可求AB
在直角三角形ABC中,BC=
在直角三角形ABDC中,BD=
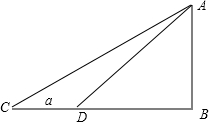
∴a=BC-BD=
-
∴AB=
∴AB+h=
+h
方案二:水平仪高为h,测量者在点C测得点A的仰角为α,向另一方向,∠CBD=γ,前进am,到达点D测得点A的仰角为β,则可求AB
在直角三角形ABC中,BC=
在直角三角形ABDC中,BD=
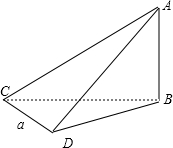
在△BCD中,a2=BC2+BD2-2×BC×BD×cosγ
=(
)2+(
)2-2×
×
×cosγ
∴AB=
∴AB+h=
+h
方案一:水平仪高为h,测量者在点C测得点A的仰角为α,前进am,到达点D测得点A的仰角为β,则可求AB
在直角三角形ABC中,BC=
| AB |
| tanα |
在直角三角形ABDC中,BD=
| AB |
| tanβ |

∴a=BC-BD=
| AB |
| tanα |
| AB |
| tanβ |
∴AB=
| atanαtanβ |
| tanβ-tanα |
∴AB+h=
| atanαtanβ |
| tanβ-tanα |
方案二:水平仪高为h,测量者在点C测得点A的仰角为α,向另一方向,∠CBD=γ,前进am,到达点D测得点A的仰角为β,则可求AB
在直角三角形ABC中,BC=
| AB |
| tanα |
在直角三角形ABDC中,BD=
| AB |
| tanβ |

在△BCD中,a2=BC2+BD2-2×BC×BD×cosγ
=(
| AB |
| tanα |
| AB |
| tanβ |
| AB |
| tanα |
| AB |
| tanβ |
∴AB=
| atanαtanβ | ||
|
∴AB+h=
| atanαtanβ | ||
|
点评:本题以实际问题为载体,考查利用正弦定理与余弦定理解决实际问题,考查方案的设计,具有开放性,值得思考

练习册系列答案
相关题目