题目内容
(14分)已知等差数列![]() 满足
满足![]() ;又数列
;又数列![]() 满足
满足![]() +…+
+…+![]() ,其中
,其中![]() 是首项为1,公比为
是首项为1,公比为![]() 的等比数列的前
的等比数列的前![]() 项和。
项和。
(I)求![]() 的表达式;
的表达式;
(Ⅱ)若![]() ,试问数列
,试问数列![]() 中是否存在整数
中是否存在整数![]() ,使得对任意的正整数
,使得对任意的正整数![]() 都有
都有![]() 成立?并证明你的结论。
成立?并证明你的结论。
解析:(I)设![]() 的首项为
的首项为![]() ,公差为d,于是由
,公差为d,于是由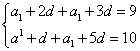
解得![]()
![]()
(Ⅱ)![]()
由![]() ①
①
得![]() ②
②
①―②得![]() 即
即![]()
当![]() 时,
时,![]() ,当
,当![]() 时,
时,![]()
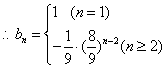
于是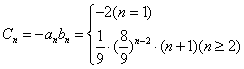
设存在正整数![]() ,使对
,使对![]() 恒成立
恒成立
当![]() 时,
时,![]() ,即
,即![]()
当![]() 时,
时,![]()
![]()
![]() 当
当![]() 时,
时,![]() 当
当![]() 时,
时,![]() ,当
,当![]() 时,
时,![]()
![]() 存在正整数
存在正整数![]() 或8,对于任意正整数
或8,对于任意正整数![]() 都有
都有![]() 成立。
成立。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目