题目内容
我们用符号“||”定义过一些数字概念，如实数绝对值的概念：对于a∈R，|a|=
，可以证明，对任意a，b∈R，不等式|a|-|b|≤|a+b|≤|a|+|b|成立．
（1）再写出两个这类数学概念的定义及其成立的不等式；
（2）对于集合A，定义“|A|”为集合A中元素的个数，对任意的集合A、B有类似的不等式成立吗？如果有，写出一个，并指出等号成立的条件（不必说明理由）；如果没有，请说明理由；
（3）设有集合A、B，若|A|=15，|B|≥15，若从A中任取两上元素，恰好都是B中元素的概率p≥
，求|A∩B|的取值范围．
|
（1）再写出两个这类数学概念的定义及其成立的不等式；
（2）对于集合A，定义“|A|”为集合A中元素的个数，对任意的集合A、B有类似的不等式成立吗？如果有，写出一个，并指出等号成立的条件（不必说明理由）；如果没有，请说明理由；
（3）设有集合A、B，若|A|=15，|B|≥15，若从A中任取两上元素，恰好都是B中元素的概率p≥
| 1 |
| 5 |
分析：（1）对于条件中定义的绝对值的意义，写出两个符合这种条件的表达式，一个是复数具有这种性质，一个是向量具有这种性质．
（2）对任意集合A，B，不等式|A|-|B|≤A∪B≤|A|+|B|成立，左边等号成立的条件是：B=φ，右边等号成立的条件是：A∩B=φ．
（3）根据所给的概率的值，表示出概率的表示式，整理出关于n的不等式即n（n-1）≥42，得到n≥7或n≤-6
注意到n≤15，n∈N，所以7≤n≤15，且n∈N，得到结果．
（2）对任意集合A，B，不等式|A|-|B|≤A∪B≤|A|+|B|成立，左边等号成立的条件是：B=φ，右边等号成立的条件是：A∩B=φ．
（3）根据所给的概率的值，表示出概率的表示式，整理出关于n的不等式即n（n-1）≥42，得到n≥7或n≤-6
注意到n≤15，n∈N，所以7≤n≤15，且n∈N，得到结果．
解答：解：（1）①设复数z=a+bi（a，b∈R），定义复数z的模为：
|z|=
（2分）
对任意复数z1，z2，不等式|z1|-|z2|≤|z1-z2|≤|z1|+|z2|成立
（也可以是||z1|-|z2||≤|z1+z2|≤|z1|+|z2|等）
②平面向量之间具有这种关系，设平面向量
={x，y}，定义向量的模为：|a|=
（5分）
对于任意向量|
|-|
|≤|
-
|≤|
|+|
成立
（2）有，对任意集合A，B，不等式|A|-|B|≤A∪B≤|A|+|B|成立（2分）
左边等号成立的条件是：B=φ，右边等号成立的条件是：A∩B=φ；（4分）
（或者：不等式||A|-|B||≤A∪B≤|A|+|B|成立（2分）
左边等号成立的条件是：B=φ 或A=φ，右边等号成立的条件是：A∩B=φ；（4分））
（3）易知：|A∩B|≤15，设|A∩B|=n，（1分）
依题意：p=
≥
，（3分）
即n（n-1）≥42，∴n≥7或n≤-6 （4分）
注意到n≤15，n∈N，所以7≤n≤15，且n∈N
即满足题意的|A∩B|的取值范围是{n|7≤n≤15，且n∈N }（6分）
|z|=
| a2+b2 |
对任意复数z1，z2，不等式|z1|-|z2|≤|z1-z2|≤|z1|+|z2|成立
（也可以是||z1|-|z2||≤|z1+z2|≤|z1|+|z2|等）
②平面向量之间具有这种关系，设平面向量
. |
| a |
| x2+y2 |
对于任意向量|
| a |
| b |
| a |
| b |
| a |
| b| |
（2）有，对任意集合A，B，不等式|A|-|B|≤A∪B≤|A|+|B|成立（2分）
左边等号成立的条件是：B=φ，右边等号成立的条件是：A∩B=φ；（4分）
（或者：不等式||A|-|B||≤A∪B≤|A|+|B|成立（2分）
左边等号成立的条件是：B=φ 或A=φ，右边等号成立的条件是：A∩B=φ；（4分））
（3）易知：|A∩B|≤15，设|A∩B|=n，（1分）
依题意：p=
| ||
|
| 1 |
| 5 |
即n（n-1）≥42，∴n≥7或n≤-6 （4分）
注意到n≤15，n∈N，所以7≤n≤15，且n∈N
即满足题意的|A∩B|的取值范围是{n|7≤n≤15，且n∈N }（6分）
点评：本题是一个新定义问题，帮助我们对于数学中有联系的知识点进行比较，本题解题的关键是读懂题目所给的条件，并且能够意义知识点写出符合条件的式子，本题是一个难题．
练习册系列答案
阅读快车系列答案
相关题目
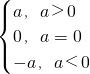，可以证明，对任意a，b∈R，不等式|a|-|b|≤|a+b|≤|a|+|b|成立．
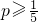，求|A∩B|的取值范围．
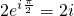；②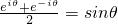
；③eiπ+1=0．以上结论中，正确结论的序号是