题目内容
过点P(2,1)的直线l被圆x2+y2=10截得的弦长为2| 5 |
分析:过点P(2,1)的直线l,要分两种情况进行讨论,斜率存在和不存在;当斜率不存在时直线方程为x=2,进行验证可得结论,过点P(2,1)的直线l,当斜率存在时,直线方程被圆x2+y2=10截得的弦长要为2
,利用垂径定理,只要满足圆心(0,0)到直线的距离为
即可,从而求出斜率k.
| 5 |
| 5 |
解答:解:过点P(2,1)的直线l,当斜率不存在时直线方程为x=2,
这时验证,被圆x2+y2=10截得的弦长显然不为为2
.这不合题意.
过点P(2,1)的直线l,当斜率存在时,直线方程为y=K(x-2)+1,
这时,被圆x2+y2=10截得的弦长要为2
,只要满足圆心(0,0)到直线的距离为
即可.
即有等式为
=
.
解得k=2,
故所求的直线方程为 x+y-5=0.
这时验证,被圆x2+y2=10截得的弦长显然不为为2
| 5 |
过点P(2,1)的直线l,当斜率存在时,直线方程为y=K(x-2)+1,
这时,被圆x2+y2=10截得的弦长要为2
| 5 |
| 5 |
即有等式为
| [-2k+1] | ||
|
| 5 |
解得k=2,
故所求的直线方程为 x+y-5=0.
点评:解决直线与圆的问题,要充分利用圆的几何性质,数形结合加以解决.

练习册系列答案
 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案 新活力总动员暑系列答案
新活力总动员暑系列答案
相关题目

 椭圆E:
椭圆E: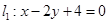 与
与 的交点为P,直
的交点为P,直 的方程为:
的方程为: .
.