题目内容
已知
是以
为周期的偶函数，且
时，
，则当
时，等于 （ ）
A． | B． | C． | D． |
B
解析试题分析：因为是以为周期的偶函数，所以当时，
所以
.
考点：本小题主要考查函数的奇偶性、周期性等性质的应用和函数解析式的求法，考查学生应用函数性质解决问题的能力.
点评：解决此类问题，要注意“求谁设谁”的原则.
练习册系列答案
相关题目
在
中，内角
所对的边分别是
. 若
，
，
，则
| A．2 | B．3 | C．4 | D．6 |
化简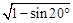
的结果是（ ）
A． | B． | C． | D． |
已知
（ ）
A． | B． | C． | D．2 |
设
,且
,则（ ）
A． | B． |
C． | D． |
在
中，角
所对的边分别为
，已知
，
，
，则
（ ）
A． | B． | C．或 | D． |
定义运算：
，则
的值是( )
A． | B． | C． | D． |
若
，则函数
的最大值和最小值为 （ ）
A．最大值为2，最小值为 ； | B．最大值为2，最小值为0； |
| C．最大值为2，最小值不存在； | D．最大值7，最小值为-5； |
已知
则
的值为 （ ）
A． | B． | C． | D． |