题目内容
(理)已知函数 ,P1(x1,y1)、P2(x2,y2)是f(x)图象上两点.
,P1(x1,y1)、P2(x2,y2)是f(x)图象上两点.(1)若x1+x2=1,求证:y1+y2为定值;
(2)设
 ,其中n∈N*且n≥2,求Tn关于n的解析式;
,其中n∈N*且n≥2,求Tn关于n的解析式;(3)对(2)中的Tn,设数列{an}满足a1=2,当n≥2时,an=4Tn+2,问是否存在角a,使不等式
 …
… 对一切n∈N*都成立?若存在,求出角α的取值范围;若不存在,请说明理由.
对一切n∈N*都成立?若存在,求出角α的取值范围;若不存在,请说明理由.
【答案】分析:(1)根据题:y1=f(x1),y2=f(x2),将f(x1)和f(x2)用函数表达式代入,利用对数的运算法则将它们相加,再化简可得y1+y2=log22=1(定值),问题得证;
(2)根据(1)的结论可得: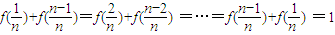 ,因此可以将Tn按倒序的方法相加的排列,再将此式与原表达式相加,最后配成n-1对数的和,每一对数的和都等于1,因而可得
,因此可以将Tn按倒序的方法相加的排列,再将此式与原表达式相加,最后配成n-1对数的和,每一对数的和都等于1,因而可得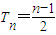 ;
;
(3)将不等式的两边都乘以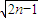 ,可得左边等于
,可得左边等于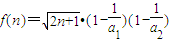 …
…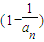 ,在(2)的基础上可得f(n)各项为正数,因此用作商相除的方法探求其单调性.证到
,在(2)的基础上可得f(n)各项为正数,因此用作商相除的方法探求其单调性.证到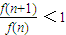 ,可得f(n+1)<f(n),所以f(n)随着n的增大而减小.不等式变形为f(1)<sinα对一切n∈N*恒成立,得到
,可得f(n+1)<f(n),所以f(n)随着n的增大而减小.不等式变形为f(1)<sinα对一切n∈N*恒成立,得到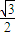 <sinα,因此可得角α的取值范围.
<sinα,因此可得角α的取值范围.
解答:解:(1)当x1+x2=1时,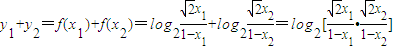 =
=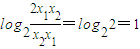 ,所以y1+y2为定值1.…(4分)
,所以y1+y2为定值1.…(4分)
(2)由(1)得,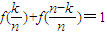 (k=1,2,…,n-1),…(6分)
(k=1,2,…,n-1),…(6分)
所以,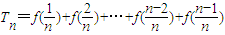 ,
,
又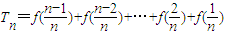 ,
,
于是2Tn=(n-1)×1,所以 (n∈N*,n≥2).…(10分)
(n∈N*,n≥2).…(10分)
(3)由已知,an=2n,n∈N*.…(11分)
由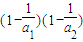 …
…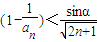 ,得
,得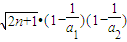 …
…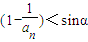 ,
,
令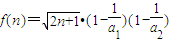 …
…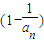 ,则由题意可得f(n)>0,
,则由题意可得f(n)>0,
于是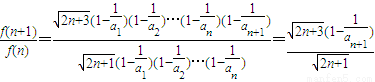
=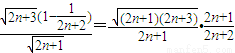 =
=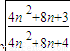 <1
<1
所以f(n+1)<f(n),即f(n)随着n的增大而减小.…(15分)
所以当n∈N*时,f(n)的最大值为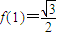 ,
,
若存在角α满足要求,则必须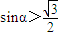 .…(16分)
.…(16分)
所以角α的取值范围为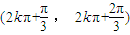 ,(k∈Z)…(18分)
,(k∈Z)…(18分)
点评:本题是一道综合题,解题的过程中用到了倒序相加法求和、用作商的方法证明数列的单调性和证明不等式恒成立等等知识点,属于难题.本题对函数与数列的一些高级处理有比较高的要求,考查的知识点与方法较多,综合性较强.
(2)根据(1)的结论可得:
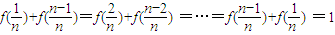 ,因此可以将Tn按倒序的方法相加的排列,再将此式与原表达式相加,最后配成n-1对数的和,每一对数的和都等于1,因而可得
,因此可以将Tn按倒序的方法相加的排列,再将此式与原表达式相加,最后配成n-1对数的和,每一对数的和都等于1,因而可得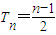 ;
;(3)将不等式的两边都乘以
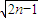 ,可得左边等于
,可得左边等于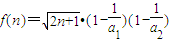 …
…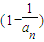 ,在(2)的基础上可得f(n)各项为正数,因此用作商相除的方法探求其单调性.证到
,在(2)的基础上可得f(n)各项为正数,因此用作商相除的方法探求其单调性.证到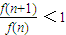 ,可得f(n+1)<f(n),所以f(n)随着n的增大而减小.不等式变形为f(1)<sinα对一切n∈N*恒成立,得到
,可得f(n+1)<f(n),所以f(n)随着n的增大而减小.不等式变形为f(1)<sinα对一切n∈N*恒成立,得到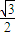 <sinα,因此可得角α的取值范围.
<sinα,因此可得角α的取值范围.解答:解:(1)当x1+x2=1时,
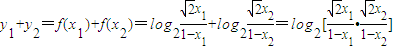 =
=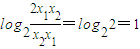 ,所以y1+y2为定值1.…(4分)
,所以y1+y2为定值1.…(4分)(2)由(1)得,
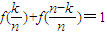 (k=1,2,…,n-1),…(6分)
(k=1,2,…,n-1),…(6分)所以,
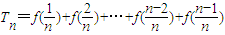 ,
,又
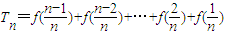 ,
,于是2Tn=(n-1)×1,所以
 (n∈N*,n≥2).…(10分)
(n∈N*,n≥2).…(10分)(3)由已知,an=2n,n∈N*.…(11分)
由
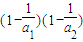 …
…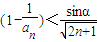 ,得
,得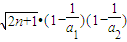 …
…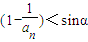 ,
,令
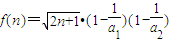 …
…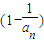 ,则由题意可得f(n)>0,
,则由题意可得f(n)>0,于是
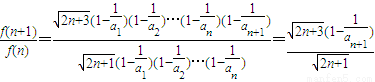
=
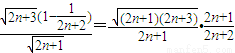 =
=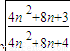 <1
<1所以f(n+1)<f(n),即f(n)随着n的增大而减小.…(15分)
所以当n∈N*时,f(n)的最大值为
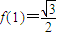 ,
,若存在角α满足要求,则必须
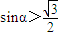 .…(16分)
.…(16分)所以角α的取值范围为
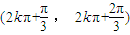 ,(k∈Z)…(18分)
,(k∈Z)…(18分)点评:本题是一道综合题,解题的过程中用到了倒序相加法求和、用作商的方法证明数列的单调性和证明不等式恒成立等等知识点,属于难题.本题对函数与数列的一些高级处理有比较高的要求,考查的知识点与方法较多,综合性较强.

练习册系列答案
相关题目
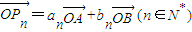 ,O为坐标原点,其中{an}、{bn}分别为等差数列和等比数列,P1是线段AB的中点,对于给定的公差不为零的an,都能找到唯一的一个bn,使得P1,P2,P3,…,Pn,…,都在一个指数函数 (写出函数的解析式)的图象上.
,O为坐标原点,其中{an}、{bn}分别为等差数列和等比数列,P1是线段AB的中点,对于给定的公差不为零的an,都能找到唯一的一个bn,使得P1,P2,P3,…,Pn,…,都在一个指数函数 (写出函数的解析式)的图象上.