题目内容
已知平面向量 不共线,且两两之间的夹角都相等,若
不共线,且两两之间的夹角都相等,若 ,则
,则 与
与 的夹角是 .
的夹角是 .
【答案】分析:由题意可得,三个向量所成的角都是120°,求出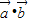 、
、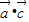 、
、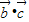 的值,即可求得
的值,即可求得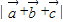 ,再利用两个向量的夹角公式求出
,再利用两个向量的夹角公式求出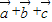 与
与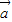 的夹角的余弦值,
的夹角的余弦值,
从而求得则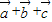 与
与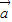 的夹角.
的夹角.
解答:解:∵平面向量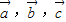 不共线,且两两之间的夹角都相等,故这3个向量两两之间的夹角都等于120°,
不共线,且两两之间的夹角都相等,故这3个向量两两之间的夹角都等于120°,
∴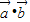 =2×2×cos120°=-2,
=2×2×cos120°=-2,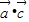 =2×1×cos120°=-1,
=2×1×cos120°=-1, =2×1×cos120°=-1,
=2×1×cos120°=-1,
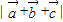 =
=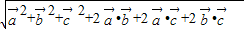 =1.
=1.
设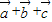 与
与 的夹角是θ,则 0°≤θ≤180°,且cosθ=
的夹角是θ,则 0°≤θ≤180°,且cosθ=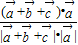 =
=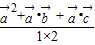 =
= ,
,
∴θ=60°,
故答案为 60°.
点评:本题考查利用向量的数量积表示向量的夹角和向量的模长公式的应用,本题解题的关键是正确利用向量的模长公式和求夹角的公式,属于中档题.
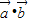 、
、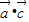 、
、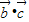 的值,即可求得
的值,即可求得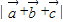 ,再利用两个向量的夹角公式求出
,再利用两个向量的夹角公式求出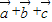 与
与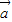 的夹角的余弦值,
的夹角的余弦值,从而求得则
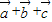 与
与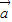 的夹角.
的夹角.解答:解:∵平面向量
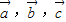 不共线,且两两之间的夹角都相等,故这3个向量两两之间的夹角都等于120°,
不共线,且两两之间的夹角都相等,故这3个向量两两之间的夹角都等于120°,∴
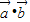 =2×2×cos120°=-2,
=2×2×cos120°=-2,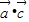 =2×1×cos120°=-1,
=2×1×cos120°=-1, =2×1×cos120°=-1,
=2×1×cos120°=-1,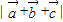 =
=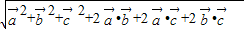 =1.
=1.设
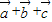 与
与 的夹角是θ,则 0°≤θ≤180°,且cosθ=
的夹角是θ,则 0°≤θ≤180°,且cosθ=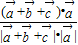 =
=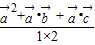 =
= ,
,∴θ=60°,
故答案为 60°.
点评:本题考查利用向量的数量积表示向量的夹角和向量的模长公式的应用,本题解题的关键是正确利用向量的模长公式和求夹角的公式,属于中档题.

练习册系列答案
 优生乐园系列答案
优生乐园系列答案
相关题目
 不共线,且两两之间的夹角都相等,若
不共线,且两两之间的夹角都相等,若 ,则
,则 与
与 的夹角是
▲ .
的夹角是
▲ .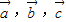 不共线,且两两之间的夹角都相等,若
不共线,且两两之间的夹角都相等,若 ,则
,则 与
与 的夹角是 .
的夹角是 . 不共线,且两两之间的夹角都相等,若
不共线,且两两之间的夹角都相等,若 ,则
,则 与
与 的夹角是 .
的夹角是 . 不共线,且两两之间的夹角都相等,若
不共线,且两两之间的夹角都相等,若 ,则
,则 与
与 的夹角是 .
的夹角是 .