题目内容
已知圆锥内切球的面积等于底面积与侧面积和的一半，求母线与底面夹角的正弦值.
解析:圆锥的轴截面是等腰三角形，球的大圆O恰是△ABC的内切圆，设圆锥的母线为l,底面半径为r,球半径为R，母线和底面夹角为2θ，则r=Rcotθ，l=
.
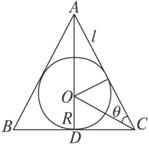
则有4πR2=
，
化简整理得（3cos2θ-2）2=0，
∴cos2θ=
，sin2θ=
.
∴sin2θ=2sinθ·cosθ=
.
∴母线与底面夹角的正弦值是
.
练习册系列答案
相关题目
题目内容
已知圆锥内切球的面积等于底面积与侧面积和的一半，求母线与底面夹角的正弦值.
解析:圆锥的轴截面是等腰三角形，球的大圆O恰是△ABC的内切圆，设圆锥的母线为l,底面半径为r,球半径为R，母线和底面夹角为2θ，则r=Rcotθ，l=.
则有4πR2=，
化简整理得（3cos2θ-2）2=0，
∴cos2θ=，sin2θ=.
∴sin2θ=2sinθ·cosθ=.
∴母线与底面夹角的正弦值是.
半径为1的球内切于圆锥（直圆锥），已知圆锥母线与底面夹角为2θ．
，则此圆锥的内切球的体积与圆锥体积之比是：