题目内容
已知向量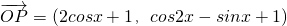 ,
,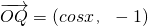 ,定义
,定义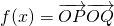
(1)求出的解析式.当时,它可以表示一个振动量,请指出其振幅,相位及初相.
(2)f(x)的图象可由y=sinx的图象怎样变化得到?
(3)设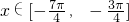 时f(x)的反函数为f-1(x),求
时f(x)的反函数为f-1(x),求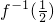 的值.
的值.
解:(1)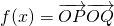 =(2cosx+1,cos2x-sinx+1)•(cosx,-1)
=(2cosx+1,cos2x-sinx+1)•(cosx,-1)
=2cos2x+cosx-cos2x+sinx-1
=sinx+cosx
= sin(x+
sin(x+ ).
).
其振幅为 ,相位为x+
,相位为x+ ,初相为
,初相为 ,
,
(2)可由y=sinx图象横坐标不变,纵坐标伸长到原来的 倍,
倍,
再把曲线上的所有点向左平移 单位,
单位,
就得到y= 的图象.
的图象.
(3)不妨设f-1( )=t,t∈[
)=t,t∈[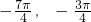 ],
],
则f(t)= ,即
,即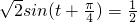
∴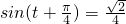
∵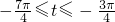
∴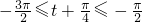 ,
,
∴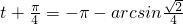 ,
,
∴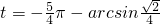
即f-1( )=
)=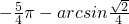 .
.
分析:(1)通过向量的数量积、二倍角公式两角和的正弦函数、化简函数为一个角的一个三角函数的形式,即可求出其振幅,相位及初相.
(2)利用左加右减的原则,通过左右平移,伸缩变换即可由y=sinx的图象得到f(x)的图象;
(3)求出f(x)的反函数为f-1(x)的表达式,即可通过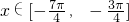 ,求出
,求出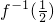 的值.
的值.
点评:本题是中档题,考查向量的数量积的应用,三角函数的基本关系式的应用,考查计算能力,转化思想.
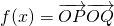 =(2cosx+1,cos2x-sinx+1)•(cosx,-1)
=(2cosx+1,cos2x-sinx+1)•(cosx,-1)=2cos2x+cosx-cos2x+sinx-1
=sinx+cosx
=
 sin(x+
sin(x+ ).
).其振幅为
 ,相位为x+
,相位为x+ ,初相为
,初相为 ,
,(2)可由y=sinx图象横坐标不变,纵坐标伸长到原来的
 倍,
倍,再把曲线上的所有点向左平移
 单位,
单位,就得到y=
 的图象.
的图象.(3)不妨设f-1(
 )=t,t∈[
)=t,t∈[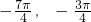 ],
],则f(t)=
 ,即
,即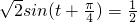
∴
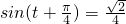
∵
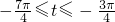
∴
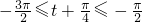 ,
,∴
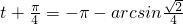 ,
,∴
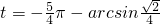
即f-1(
 )=
)=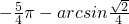 .
.分析:(1)通过向量的数量积、二倍角公式两角和的正弦函数、化简函数为一个角的一个三角函数的形式,即可求出其振幅,相位及初相.
(2)利用左加右减的原则,通过左右平移,伸缩变换即可由y=sinx的图象得到f(x)的图象;
(3)求出f(x)的反函数为f-1(x)的表达式,即可通过
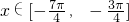 ,求出
,求出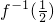 的值.
的值.点评:本题是中档题,考查向量的数量积的应用,三角函数的基本关系式的应用,考查计算能力,转化思想.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案
相关题目
 ,
, ,定义
,定义
 ,
, ,定义
,定义
 ,
, ,定义
,定义
 ,
, ,定义
,定义 .
. 的解析式.当
的解析式.当 时,它可以表示一个振动量,请指出其振幅,相位及初相.
时,它可以表示一个振动量,请指出其振幅,相位及初相. 的图像怎样变化得到?
的图像怎样变化得到? 且
且 为△ABC的一个内角,求
为△ABC的一个内角,求 ,
, ,定义
,定义
 的解析式.当
的解析式.当 时,它可以表示一个振动量,请指出其振幅,相位及初相.
时,它可以表示一个振动量,请指出其振幅,相位及初相. 的图像怎样变化得到?
的图像怎样变化得到? 时
时 ,求
,求 的值.
的值.