题目内容
有一组观测数据(x1,y1),(x2,y2),…,(x12,y12)得
=1.542,
=2.8475,
=29.808,
=99.208,
xiyi=54.243,则回归直线方程是
=1.218x+0.969
=1.218x+0.969.
. |
| x |
. |
| y |
| n |
 |
| i=1 |
| x | 2 i |
| n |
 |
| i=1 |
| y | 2 i |
| n |
 |
| i=1 |
| ? |
| y |
| ? |
| y |
分析:根据回归直线斜率公式求出直线的斜率的估计值是1.218,得到线性回归方程是y=1.218x+b,根据横标和纵标的值得到样本中心点,把中心点代入方程求出b的值.
解答:解:
=1.542
=2.8475
利用公式可得
=
=1.218,
又
=
-
=0.969.
∴回归方程是
=1.218x+0.969
故答案为
=1.218x+0.969
. |
| x |
. |
| y |
利用公式可得
 |
| b |
| |||||||
|
又
 |
| a |
. |
| y |
 |
| b |
. |
| x |
∴回归方程是
| ? |
| y |
故答案为
| ? |
| y |
点评:本题考查线性回归方程的写法,解题的关键是知道线性回归直线一定过样本中心点,把样本中心点代入求出b的值,注意数字的运算.

练习册系列答案
 优加精卷系列答案
优加精卷系列答案
相关题目
 :,且x1+x2+x3+…+x8=2(y1+y2+y3+…+y8)=6,则实数a的值是( )
:,且x1+x2+x3+…+x8=2(y1+y2+y3+…+y8)=6,则实数a的值是( ) B.
B. C.
C. D.
D.
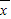 =1.542,
=1.542,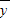 =2.8475,
=2.8475,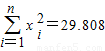 ,
,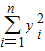 =99.208,
=99.208,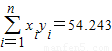 ,则回归直线方程是 .
,则回归直线方程是 .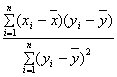 B.
B. 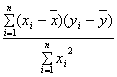
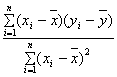 D.
D.