题目内容
古汉集团生产的A,B两种型号的口服液供出口,国家为鼓励产品出口,采用出口退税政策:出口价值为a万元的/1产品可获得| 1 |
| 10 |
(1)当m=
| 8 |
| 5 |
(精确到0.1,参考数据:ln2≈0.7)
(2)记该企业获得的退税款的最大值函数为,f(m),求f(m)的表达式.
分析:(1)先设出口B产品价值x万元,该企业获得的退税款为y万元.可得y=mln(x+1)+
(100-x) 10≤x≤100,,把m=
代入求出其导函数,研究出其在定义域上的单调性即可求出其最大值;
(2)先求出导数为0的根x=10m-1,再把x=10m-1与区间的位置关系分三种情况讨论,分别得到其在定义域上的单调性进而求出其最大值.
| 1 |
| 10 |
| 8 |
| 5 |
(2)先求出导数为0的根x=10m-1,再把x=10m-1与区间的位置关系分三种情况讨论,分别得到其在定义域上的单调性进而求出其最大值.
解答:解:(1)设出口B产品价值x万元,则出口A产品价值为(100-x)万元,设该企业获得的退税款为y万元.
则y=mln(x+1)+
(100-x) 10≤x≤100,
当m=
时,y=
ln(x+1)+
(100-x)
由y'=
-
得x=15
易知:当x∈(10,15)时函数递增,
当x∈(15,90)时,函数递减.
故当x=15时,ymax=
ln16+
×85≈13.0
(2)由y=mln(x+1)+
(100-x)
得y'=
-
令y′=0得x=10m-1,
①当0<10m-1<10时,即0.1<m<1.1
此时函数在(10,90)上单调递减,故f(m)=f(10)=9+mln11.
当10≤10m-1≤90时,即1.1≤m≤9.1
此时,函数在(10,10m-1)上递增,在(10m-1,90)上递减.
故f(m)=f(10m-1)=mln10m-m+10.1
当10m-1>90时,即m>9.1,
此时函数在(10,90)上递增,
故f(m)=f(90)=mln91+1
综上f(m)=
.
则y=mln(x+1)+
| 1 |
| 10 |
当m=
| 8 |
| 5 |
| 8 |
| 5 |
| 1 |
| 10 |
由y'=
| 8 |
| 5(x+1) |
| 1 |
| 10 |
易知:当x∈(10,15)时函数递增,
当x∈(15,90)时,函数递减.
故当x=15时,ymax=
| 8 |
| 5 |
| 1 |
| 10 |
(2)由y=mln(x+1)+
| 1 |
| 10 |
得y'=
| m |
| x+1 |
| 1 |
| 10 |
令y′=0得x=10m-1,
①当0<10m-1<10时,即0.1<m<1.1
此时函数在(10,90)上单调递减,故f(m)=f(10)=9+mln11.
当10≤10m-1≤90时,即1.1≤m≤9.1
此时,函数在(10,10m-1)上递增,在(10m-1,90)上递减.
故f(m)=f(10m-1)=mln10m-m+10.1
当10m-1>90时,即m>9.1,
此时函数在(10,90)上递增,
故f(m)=f(90)=mln91+1
综上f(m)=
|
点评:本题主要考查函数在日常生活中的应用以及分段函数的应用.做函数应用题的关键是,把文字语言转化为数学语言,用数学知识来解题.

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目
 万元的退税款,出口价值为b万元的B产品可获得mln(b+1)(m>0)万元的退税款.已知厂家出口总价值为100万元的A、B两种口服液,且两种口服液的出口价值都不低于10万元.
万元的退税款,出口价值为b万元的B产品可获得mln(b+1)(m>0)万元的退税款.已知厂家出口总价值为100万元的A、B两种口服液,且两种口服液的出口价值都不低于10万元. 时,请你制定一个方案,使得在这次出口贸易中该企业获得的退税款最多,并求出其最大值;
时,请你制定一个方案,使得在这次出口贸易中该企业获得的退税款最多,并求出其最大值;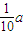 万元的退税款,出口价值为b万元的B产品可获得mln(b+1)(m>0)万元的退税款.已知厂家出口总价值为100万元的A、B两种口服液,且两种口服液的出口价值都不低于10万元.
万元的退税款,出口价值为b万元的B产品可获得mln(b+1)(m>0)万元的退税款.已知厂家出口总价值为100万元的A、B两种口服液,且两种口服液的出口价值都不低于10万元.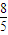 时,请你制定一个方案,使得在这次出口贸易中该企业获得的退税款最多,并求出其最大值;
时,请你制定一个方案,使得在这次出口贸易中该企业获得的退税款最多,并求出其最大值; 万元的退税款,出口价值为b万元的B产品可获得mln(b+1)(m>0)万元的退税款.已知厂家出口总价值为100万元的A、B两种口服液,且两种口服液的出口价值都不低于10万元.
万元的退税款,出口价值为b万元的B产品可获得mln(b+1)(m>0)万元的退税款.已知厂家出口总价值为100万元的A、B两种口服液,且两种口服液的出口价值都不低于10万元. 时,请你制定一个方案,使得在这次出口贸易中该企业获得的退税款最多,并求出其最大值;
时,请你制定一个方案,使得在这次出口贸易中该企业获得的退税款最多,并求出其最大值;