题目内容
(12分)已知函数 为奇函数,
为奇函数, 为常数,
为常数,
(1)求实数 的值;
的值;
(2)证明:函数 在区间
在区间 上单调递增;
上单调递增;
(3)若对于区间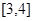 上的每一个
上的每一个 值,不等式
值,不等式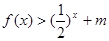 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
【答案】
(1)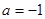 ;(3)
;(3)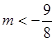 .
.
【解析】
试题分析:(1)根据f(x)为奇函数,所以f(-x)+f(x)=0恒成立,所以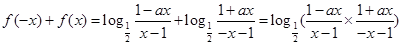
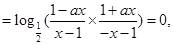
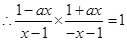 ,
,
所以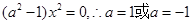 ,经检验当a=1时,显然不符合要求,
,经检验当a=1时,显然不符合要求,
所以a=-1.
(2)证明:设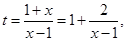
设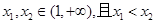 ,
,
所以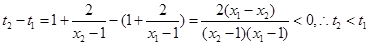 ,
,
所以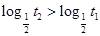
即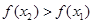 ,
,
所以函数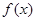 在区间
在区间 上单调递增;
上单调递增;
(3) 对于区间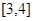 上的每一个
上的每一个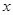 值,不等式
值,不等式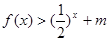 恒成立,
恒成立,
即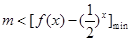 ,由(2)知
,由(2)知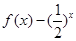 在[3,4]上是增函数,所以当x=3时,
在[3,4]上是增函数,所以当x=3时,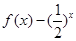 取得最小值,最小值为
取得最小值,最小值为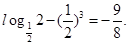
所以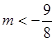 .
.
考点:函数的奇偶性,复合函数的单调性证明,函数单调性在不等式恒成立问题中的应用.
点评:函数是奇偶性可知f(-x)+f(x)=0恒成立,这是求解析式参数的基本方法.
复合函数单调性的证明可先证明内函数的单调性,再根据外函数的单调性证明即可,同学们要认真体会本小题的证法.
不等式恒成立问题在参数与变量能分离的情况下,最好分离参数,然后转化为函数最值求解.

练习册系列答案
 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案
相关题目
 为奇函数,则下列结论正确的是( )
为奇函数,则下列结论正确的是( )
 为奇函数,且为增函数, 则函
为奇函数,且为增函数, 则函 的图象为 ( )
的图象为 ( )
 为奇函数,
为奇函数, 为偶函数,且
为偶函数,且 .
. ,则称
,则称 是函数
是函数