题目内容
已知函数
 是奇函数,又f(1)=2,f(2)<3.
是奇函数,又f(1)=2,f(2)<3.
(1)求
a,b,c的值;(2)
判断f(x)在 上的单调性.
上的单调性.
答案:略
解析:
解析:
|
(1) 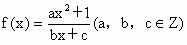 是奇函数, 是奇函数,
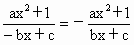 ,即-bx+c=-bx-c. ,即-bx+c=-bx-c.
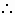 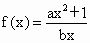 . .
又 f(1)=2,故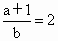 . .
而 f(2)<3,即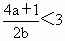 ,即 ,即 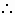 -1<a<2. -1<a<2.
又由于 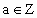 , ,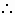 a=0或a=1. a=0或a=1.
当 a=0时, (舍);当a=1时,b=1. (舍);当a=1时,b=1.
综上可知, a=b=1,c=0.(2) 设 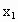 、 、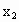 是 是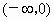 上的任意两个实数,且 上的任意两个实数,且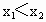 ,则 ,则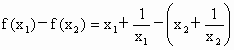
当 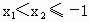 时, 时,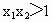 , ,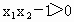 ,从而 ,从而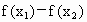 <0, <0,
即 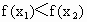 .所以函数 .所以函数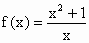 在 在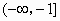 上为函数. 上为函数.
当 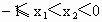 时, 时,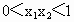 , ,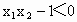 从而 从而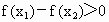 ,即 ,即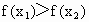 . .
所以函数 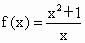 在[-1,0)上为减函数. 在[-1,0)上为减函数.
函数的单调性、奇偶性是函数的重要性质,这两部分内容及函数其他性质经常组合在一起,出现一些难度较大的综合题. |

练习册系列答案
相关题目
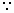
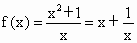
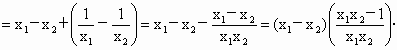
 是奇函数,又f(1)=2,f(2)<3,且f(x)在[1,+∞)上递增.
是奇函数,又f(1)=2,f(2)<3,且f(x)在[1,+∞)上递增. (x2+x+
(x2+x+ )]<f[
)]<f[ )]的解.
)]的解. 是奇函数,又
是奇函数,又 .
. 是奇函数,又
是奇函数,又 .
.