题目内容
已知函数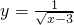 的定义域为集合A,y=-x2+a2+2a的值域为集合B.
的定义域为集合A,y=-x2+a2+2a的值域为集合B.
(1)若a=2,求A∩B;
(2)若A∪B=R,求实数a的取值范围.
解:函数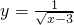 的定义域A={x|x>3},
的定义域A={x|x>3},
y=-x2+a2+2a的值域为B={x|x≤a2+2a}
(1)当a=2时,B={x|x≤8}
此时A∩B={x|3<x≤8}
(2)要使A∪B=R,需要a2+2a≥3,
解得a≤-3,或a≥1
故使A∪B=R的实数a的取值范围为a≤-3,或a≥1
分析:根据函数解析式有意义的原则可以求出集合A,根据实数的性质可以求出集合B
(1)将a=2代入集合B,结合集合交集运算法则可得答案.
(2)根据A∪B=R,可构造关于a的不等式组a2+2a≥3,解不等式可得实数a的取值范围.
点评:本题考查的知识点是函数的定义域,函数的值域,集合的交集、并集运算,其中求出集合A,B是解答的关键.
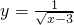 的定义域A={x|x>3},
的定义域A={x|x>3},y=-x2+a2+2a的值域为B={x|x≤a2+2a}
(1)当a=2时,B={x|x≤8}
此时A∩B={x|3<x≤8}
(2)要使A∪B=R,需要a2+2a≥3,
解得a≤-3,或a≥1
故使A∪B=R的实数a的取值范围为a≤-3,或a≥1
分析:根据函数解析式有意义的原则可以求出集合A,根据实数的性质可以求出集合B
(1)将a=2代入集合B,结合集合交集运算法则可得答案.
(2)根据A∪B=R,可构造关于a的不等式组a2+2a≥3,解不等式可得实数a的取值范围.
点评:本题考查的知识点是函数的定义域,函数的值域,集合的交集、并集运算,其中求出集合A,B是解答的关键.

练习册系列答案
 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案
相关题目
 的定义域为
的定义域为 ,且
,且 的图像如右图所示,记
的图像如右图所示,记 ,则不等式
,则不等式 的解集是 ▲ .
的解集是 ▲ .
 的定义域为
的定义域为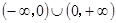 ,且满足条件:①
,且满足条件:① ,②
,② ③当
③当 .
. 的解集
的解集