题目内容
(04年湖北卷文)(12分)
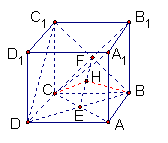
如图,在棱长为1的正方体ABCD―A1B1C1D1中,AC与BD交于点E,CB与CB1交于
点F.
(I)求证:A1C⊥平BDC1;
(II)求二面角B―EF―C的大小(结果用反三角函数值表示).

解析:解法一:(Ⅰ)∵A1A⊥底面ABCD,则AC是A1C在底面ABCD的射影.
∵AC⊥BD.∴A1C⊥BD.
同理A1C⊥DC1,又BD∩DC1=D,
∴A1C⊥平面BDC1.
(Ⅱ)取EF的中点H,连结BH、CH,

又E、F分别是AC、B1C的中点,

解法二:(Ⅰ)以点C为坐标原点建立如图所示的空间直角坐标系,
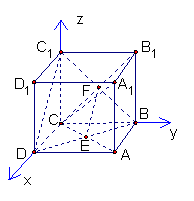
则C(0,0,0).D(1,0,0),B(0,1,0),A1(1,1,1),C1(0,0,1),D1(1,0,1)
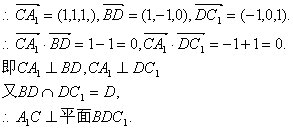
(Ⅱ)同(I)可证,BD1⊥平面AB1C.


练习册系列答案
 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目