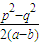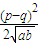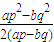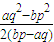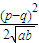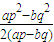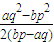题目内容
某单位退休职工每年的退休金金额与他服务年数的平方根成正比现有甲、乙、丙三名退休职工.已知乙比甲多服务a年,他的退休金比甲多p元,丙比甲多服务6年(b≠a).他的退休金比甲多q元,那么甲每年的退休金是
- A.
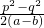
- B.
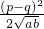
- C.
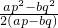
- D.
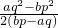
D
分析:如果设正常工作x年,退休金与服务年数的平方根的比例系数为k,则k -k
-k  =p①,k
=p①,k 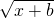 -k
-k  =q②;那么,正常退休时每年的退休金应为
=q②;那么,正常退休时每年的退休金应为 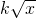 ,不妨设
,不妨设 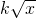 =t,则
=t,则  ,①式可化为
,①式可化为  =
=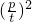 +2
+2 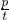 =
=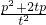 ,②式可化为
,②式可化为  =
=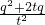 ;两式相比,得出t,即为所求.
;两式相比,得出t,即为所求.
解答:设正常工作x年,退休金与服务年数的平方根的比例系数为k,则由题意,得
k -k
-k  =p①,k
=p①,k 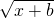 -k
-k  =q②;设
=q②;设 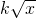 =t,则
=t,则  ,①式可化为
,①式可化为 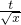 •
• -t=p,即
-t=p,即 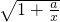 -1=
-1=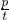 ,∴
,∴ =
=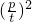 +2
+2 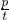 =
=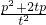 ③;
③;
同理,②式可化为 =
=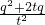 ④;
④;
③÷④,得 =
=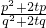 ,∴t=
,∴t=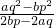 ;所以,正常退休时每年的退休金为
;所以,正常退休时每年的退休金为 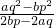 (元).
(元).
故选D.
点评:本题考查了含有二次根式的函数模型的应用,重点是考查了二次根式的运算能力,是中档题.
分析:如果设正常工作x年,退休金与服务年数的平方根的比例系数为k,则k
 -k
-k  =p①,k
=p①,k 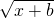 -k
-k  =q②;那么,正常退休时每年的退休金应为
=q②;那么,正常退休时每年的退休金应为 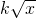 ,不妨设
,不妨设 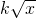 =t,则
=t,则  ,①式可化为
,①式可化为  =
=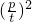 +2
+2 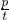 =
=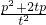 ,②式可化为
,②式可化为  =
=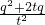 ;两式相比,得出t,即为所求.
;两式相比,得出t,即为所求.解答:设正常工作x年,退休金与服务年数的平方根的比例系数为k,则由题意,得
k
 -k
-k  =p①,k
=p①,k 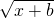 -k
-k  =q②;设
=q②;设 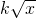 =t,则
=t,则  ,①式可化为
,①式可化为 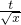 •
• -t=p,即
-t=p,即 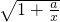 -1=
-1=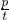 ,∴
,∴ =
=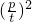 +2
+2 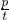 =
=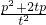 ③;
③;同理,②式可化为
 =
=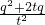 ④;
④;③÷④,得
 =
=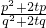 ,∴t=
,∴t=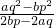 ;所以,正常退休时每年的退休金为
;所以,正常退休时每年的退休金为 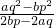 (元).
(元).故选D.
点评:本题考查了含有二次根式的函数模型的应用,重点是考查了二次根式的运算能力,是中档题.

练习册系列答案
相关题目
某单位退休职工每年的退休金金额与他服务年数的平方根成正比现有甲、乙、丙三名退休职工.已知乙比甲多服务a年,他的退休金比甲多p元,丙比甲多服务b年(b≠a).他的退休金比甲多q元,那么甲每年的退休金是( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|