Question

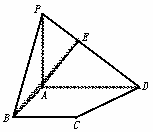
如图10-24，在四棱锥P-ABCD中，底面ABCD是一直角梯形，∠BAD＝90°，AD∥BC，AB＝BC＝a，AD＝2a且PA⊥底面ABCD，PD与底面成30°角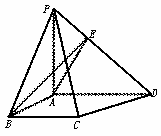

图10-24

(Ⅰ)若AE⊥PD，E为垂足，求证：BE⊥PD；

(Ⅱ)求异面直线AE与CD所成角的大小(用反三角函数表示).

Answer 1

(Ⅰ)方法一：如图10-57(1)

图10-57(1)

∵PA⊥平面ABCD，

∴PA⊥AB，再由AB⊥AD，得AB⊥平面PAD，

∴AB⊥PD．

又∵AE⊥PD，∴PD⊥平面ABE，故BE⊥PD．

 

方法二：由题设AB⊥AD，AB⊥AP，∴AB⊥平面PAD，

故由AB⊥平面PAD，AE⊥PD，得BE⊥PD.

 

（Ⅱ）方法一：如图10-57(2)，以A为原点，AB、AD、AP所在直线为坐标轴，建立空间直角坐标系，

则点C、D的坐标分别为(a,a,0),(0,2a,0).

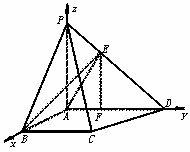
图10-57(2)

∵PA⊥平面ABCD，得∠PDA是PD与底面ABCD所成的角.

∴∠PDA＝30°，

于是在Rt△AED中，由AD＝2a，得AE＝a，

过E作EF⊥AD，垂足为F，

在Rt△AFE中，由AE＝a，∠EAF＝60°，

 

得AF＝a，EF＝a，

 

∴E(0，a，a）．

 

于是＝，＝{－a，a，0}．

 

设与的夹角为θ，

则由cosθ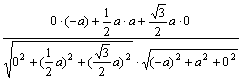＝＝＝，得θ＝arccos，

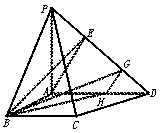
图10-57(3)

即AE与CD所成角的大小为arccos．

 

方法二：如图10-57(3)，设G、H分别为ED、AD的中点，连结BH、HG、GB，

易知DH平行且等于CB，

∴BH∥CD，

∵G、H分别为ED、AD的中点，

∴HG∥AE，

则∠BHG或它的补角就是异面直线AE、CD所成的角.

 

而HG＝，AE＝a，BH＝＝a，

 

BG²＝BE²＋EG²＝AB²＋AE²＋EG²＝a²，

 

在△BHG中，由余弦定理可得cos∠BHG＝＝－．

 

∠BHG＝π－arccos，

所以异面直线AE、CD所成角的大小为arccos．