题目内容
若方程lnx+2x-10=0的解为x0，则不小于x0的最小整数是（ ）
分析：由条件：lnx+2x-10=0得lnx=10-2x，欲求出方程的近似解，利用图解法，分别作出函数y=lnx和y=10-2x的图象，观察交点在（4，5）内．
解答：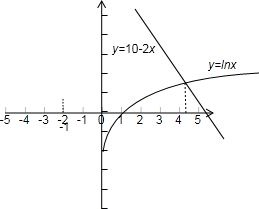
解：由条件：lnx+2x-10=0得lnx=10-2x，
分别作出函数y=lnx和y=10-2x的图象：
观察交点在（4，5）内．
则不小于x0的最小整数是5．
故选B．
解：由条件：lnx+2x-10=0得lnx=10-2x，分别作出函数y=lnx和y=10-2x的图象：
观察交点在（4，5）内．
则不小于x0的最小整数是5．
故选B．
点评：本题考查了函数的零点．考查了数形结合思想．数形结合是重要的数学思想，以形助数，直观简捷，从而利用函数图象可以进一步发现函数性质，并能利用函数图象解决实际问题．
练习册系列答案
相关题目