题目内容
若复数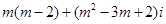 是纯虚数,则实数
是纯虚数,则实数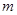 的值为( )
的值为( )
A. 或 或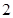 | B.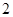 | C. | D.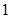 或 或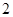 |
C
解析试题分析:由题意可知复数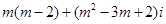 是纯虚数,则
是纯虚数,则 解得
解得 .故选C.本题的要注意纯虚数的定义,实部为零并且虚部不为零.这两条件要同时满足,往往容易漏掉虚部不为零的条件.
.故选C.本题的要注意纯虚数的定义,实部为零并且虚部不为零.这两条件要同时满足,往往容易漏掉虚部不为零的条件.
考点:1.纯虚数的概念.2.解二次方程与二次不等式.

练习册系列答案
 灵星计算小达人系列答案
灵星计算小达人系列答案
相关题目
不等式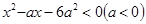 的解集为( )
的解集为( )
A.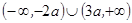 | B.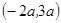 |
C.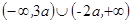 | D.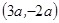 |
已知一元二次不等式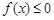 的解集为
的解集为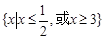 ,则
,则 的解集为( )
的解集为( )
A.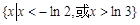 | B.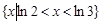 |
C.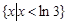 } } | D. |
已知不等式 的解集为
的解集为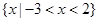 ,则不等式
,则不等式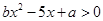 的解集为( )
的解集为( )
A. | B.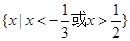 |
C.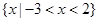 | D.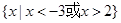 |
已知
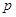 是
是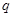 的充分条件,则实数
的充分条件,则实数 的取值范围是( )
的取值范围是( )
A.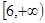 | B.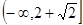 | C. | D. |
已知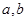 是任意实数,且
是任意实数,且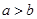 ,则下列结论正确的是( )
,则下列结论正确的是( )
A. | B.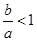 | C.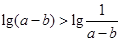 | D. |
不等式 ≤x-2的解集是( )
≤x-2的解集是( )
| A.(-∞,0]∪(2,4] | B.[0,2)∪[4,+∞) |
| C.[2,4) | D.(-∞,2]∪(4,+∞) |
若关于x的不等式ax-b>0的解集为(1,+∞),则关于x的不等式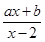 >0的解集为( )
>0的解集为( )
| A.(-1,2) |
| B.(-∞,-1)∪(2,+∞) |
| C.(1,2) |
| D.(-∞,-2)∪(1,+∞) |
已知不等式|x+2|+|x|≤a的解集不是空集,则实数a的取值范围是( ).
| A.(-∞,2) | B.(-∞,2] |
| C.(2,+∞) | D.[2,+∞) |