题目内容
 如右图,在正方体ABCD-A1B1C1D1中,M是棱DD1的中点,O为底面ABCD的中心,P为棱A1B1上任意一点,则直线OP与直线AM所成的角的大小为( )
如右图,在正方体ABCD-A1B1C1D1中,M是棱DD1的中点,O为底面ABCD的中心,P为棱A1B1上任意一点,则直线OP与直线AM所成的角的大小为( )分析:虽然直线OP为动直线,但其在平面ADD1A1上的射影是不变的,依据三垂线定理,直线AM垂直于斜线在这个平面上的射影,就垂直于这条直线,从而发现AM恒与OP垂直.
解答:解:取AD中点N,则ON⊥平面ADD1A1,A1N为OP在平面ADD1A1上的射影,
在正方形ADD1A1中,DM=AN,AD=AA1,∴Rt△A1NA≌Rt△AMD
∴AM⊥A1N
由三垂线定理可知AM⊥OP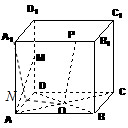
在正方形ADD1A1中,DM=AN,AD=AA1,∴Rt△A1NA≌Rt△AMD
∴AM⊥A1N
由三垂线定理可知AM⊥OP

点评:本题考查了三垂线定理的运用,解题时要有较强的空间想象力,善于发现变化中的不变关系,将空间问题转化为平面问题解决

练习册系列答案
 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案
相关题目
 A. B.
A. B.