题目内容
在二项式(1+3x)n和(2x+5)n的展开式中,各项系数之和分别记为an、bn、n是正整数,则| lim |
| n→∞ |
| an-2bn |
| 3an-4bn |
分析:先求出各项系数之和an、bn,代入所求极限表达式,再由极限运算法则可求.
解答:解:由题可知:二项式(1+3x)n和(2x+5)n的展开式中,分别令x=1即可得an=4n、bn=7n,
将an=4n、bn=7n,代入
=
=
=
,
故答案为:
将an=4n、bn=7n,代入
| lim |
| n→∞ |
| an-2bn |
| 3an-4bn |
| lim |
| n→∞ |
| 4n-2×7n |
| 3×4n- 4×7n |
| lim |
| n→∞ |
(
| ||
3×(
|
| 1 |
| 2 |
故答案为:
| 1 |
| 2 |
点评:本题有两点注意:
(1)用特殊值求二项式展开式各项系数和,高考中常在填空中出现.
(2)分式极限求解法则要熟练掌握.
(1)用特殊值求二项式展开式各项系数和,高考中常在填空中出现.
(2)分式极限求解法则要熟练掌握.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 = .
= .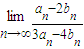 = .
= .