题目内容
若函数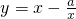 在(1,+∞)上为增函数,求实数a的取值范围.
在(1,+∞)上为增函数,求实数a的取值范围.
解:令f(x)=y=x- ,
,
则f′(x)=1+ ,
,
∵f(x)=y=x- 在(1,+∞)上为增函数,
在(1,+∞)上为增函数,
∴f′(1)=1+a≥0,
∴a≥-1.
分析:依题意可求得f′(x)=1+ ,f(x)=x-
,f(x)=x- 在(1,+∞)上为增函数,f′(1)≥0,从而得到答案.
在(1,+∞)上为增函数,f′(1)≥0,从而得到答案.
点评:本题考查函数的单调性,着重考查导数的应用,对:“f(x)=x- 在(1,+∞)上为增函数,f′(1)=1+a≥0”的理解与应用是难点,属于中档题.
在(1,+∞)上为增函数,f′(1)=1+a≥0”的理解与应用是难点,属于中档题.
 ,
,则f′(x)=1+
 ,
,∵f(x)=y=x-
 在(1,+∞)上为增函数,
在(1,+∞)上为增函数,∴f′(1)=1+a≥0,
∴a≥-1.
分析:依题意可求得f′(x)=1+
 ,f(x)=x-
,f(x)=x- 在(1,+∞)上为增函数,f′(1)≥0,从而得到答案.
在(1,+∞)上为增函数,f′(1)≥0,从而得到答案.点评:本题考查函数的单调性,着重考查导数的应用,对:“f(x)=x-
 在(1,+∞)上为增函数,f′(1)=1+a≥0”的理解与应用是难点,属于中档题.
在(1,+∞)上为增函数,f′(1)=1+a≥0”的理解与应用是难点,属于中档题. 
练习册系列答案
 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案 双基同步导航训练系列答案
双基同步导航训练系列答案 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案
相关题目