题目内容
已知函数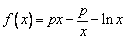 ,
,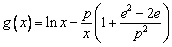 ,其中无理数
,其中无理数
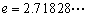 .
.
(Ⅰ)若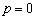 ,求证:
,求证: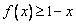 ;
;
(Ⅱ)若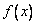 在其定义域内是单调函数,求
在其定义域内是单调函数,求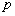 的取值范围;
的取值范围;
(Ⅲ)对于区间(1,2)中的任意常数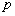 ,是否存在
,是否存在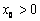 使
使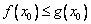 成立?
成立?
若存在,求出符合条件的一个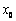 ;否则,说明理由.
;否则,说明理由.
【答案】
(Ⅰ)证明:当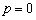 时,
时,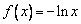 .令
.令 ,则
,则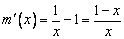 .
.
若 ,
, 递增;若
递增;若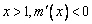 ,
, 递减,
递减,
则 是
是 的极(最)大值点.于是
的极(最)大值点.于是
 ,即
,即 .故当
.故当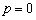 时,有
时,有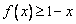 .……5分
.……5分
(Ⅱ)解:对 求导,得
求导,得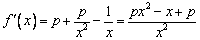 .
.
①若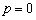 ,
, ,则
,则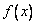 在
在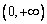 上单调递减,故
上单调递减,故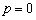 合题意.
合题意.
②若 ,
, .
.
则必须 ,故当
,故当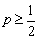 时,
时,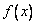 在
在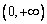 上单调递增.
上单调递增.
③若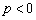 ,
, 的对称轴
的对称轴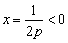 ,则必须
,则必须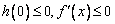 ,
,
故当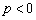 时,
时,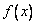 在
在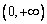 上单调递减.
上单调递减.
综合上述,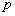 的取值范围是
的取值范围是 .……………………10分
.……………………10分
(Ⅲ)解:令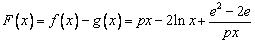 .则问题等价于
.则问题等价于
找一个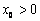 使
使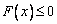 成立,故只需满足函数的最小值
成立,故只需满足函数的最小值 即可.
即可.
因 ,
,
而 ,
,
故当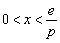 时,
时, ,
, 递减;当
递减;当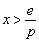 时,
时, ,
, 递增.
递增.
于是,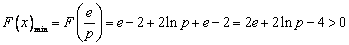 .
.
与上述要求 相矛盾,故不存在符合条件的
相矛盾,故不存在符合条件的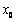 .
.

练习册系列答案
相关题目
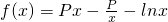 ,
,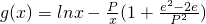 ,其中无理数e=2.17828….
,其中无理数e=2.17828….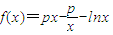 ,
,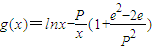 ,其中无理数e=2.17828….
,其中无理数e=2.17828…. ,
, ,其中无理数e=2.17828….
,其中无理数e=2.17828….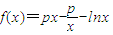 ,
, ,其中无理数e=2.17828….
,其中无理数e=2.17828….