题目内容
已知实数a≠0,给出下列命题:
①函数f(x)=asin(2x+
)的图象关于直线x=
对称;
②函数f(x)=asin(2x+
)的图象可由g(x)=asin2x的图象向左平移
个单位而得到;
③把函数h(x)=asin(x+
)的图象上的所有点的纵坐标保持不变,横坐标缩短到原来的
倍,可以得到函数f(x)=asin(2x+
)的图象;
④若函数f(x)=asin(2x+
+?)(x∈R)为偶函数,则?=kπ+
(k∈Z).
其中正确命题的序号有______;(把你认为正确的命题的序号都填上).
①函数f(x)=asin(2x+
| π |
| 3 |
| π |
| 3 |
②函数f(x)=asin(2x+
| π |
| 3 |
| π |
| 6 |
③把函数h(x)=asin(x+
| π |
| 3 |
| 1 |
| 2 |
| π |
| 3 |
④若函数f(x)=asin(2x+
| π |
| 3 |
| π |
| 6 |
其中正确命题的序号有______;(把你认为正确的命题的序号都填上).
对于①,因为x=
时,f(x)=asin(2x+
)的值是0,不是最值,故直线x=
不是函数图象的对称轴,故①不正确;
对于②,根据函数图象平移的公式,可得g(x)=asin2x的图象向左平移
个单位得到g(x+
)=asin(2x+
),所以f(x)=asin(2x+
)可由g(x)=asin2x的图象向左平移
个单位而得到,故②正确;
对于③,根据函数y=Asin(ωx+φ)图象的变换公式,得函数h(x)=asin(x+
)的图象上的所有点的纵坐标保持不变,横坐标缩短到原来的
倍,得到函数f(x)=asin(2x+
)的图象,故③正确;
对于④,若函数f(x)=asin(2x+
+?)(x∈R)为偶函数,则f(x)可以化简为acos2x或-acos2x,因此
+∅=
+kπ,解之得?=kπ+
(k∈Z),故④正确.
故答案为:②③④
| π |
| 3 |
| π |
| 3 |
| π |
| 3 |
对于②,根据函数图象平移的公式,可得g(x)=asin2x的图象向左平移
| π |
| 6 |
| π |
| 6 |
| π |
| 3 |
| π |
| 3 |
| π |
| 6 |
对于③,根据函数y=Asin(ωx+φ)图象的变换公式,得函数h(x)=asin(x+
| π |
| 3 |
| 1 |
| 2 |
| π |
| 3 |
对于④,若函数f(x)=asin(2x+
| π |
| 3 |
| π |
| 3 |
| π |
| 2 |
| π |
| 6 |
故答案为:②③④

练习册系列答案
相关题目
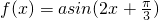 的图象关于直线
的图象关于直线 对称;
对称; 个单位而得到;
个单位而得到;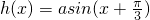 的图象上的所有点的纵坐标保持不变,横坐标缩短到原来的
的图象上的所有点的纵坐标保持不变,横坐标缩短到原来的 倍,可以得到函数
倍,可以得到函数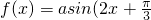 )的图象;
)的图象;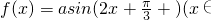 R)为偶函数,则
R)为偶函数,则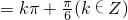 .
.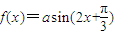 的图象关于直线
的图象关于直线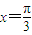 对称;
对称;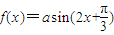 的图象可由g(x)=asin2x的图象向左平移
的图象可由g(x)=asin2x的图象向左平移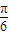 个单位而得到;
个单位而得到;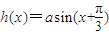 的图象上的所有点的纵坐标保持不变,横坐标缩短到原来的
的图象上的所有点的纵坐标保持不变,横坐标缩短到原来的 倍,可以得到函数
倍,可以得到函数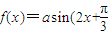 )的图象;
)的图象;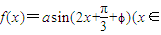 R)为偶函数,则
R)为偶函数,则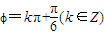 .
.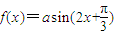 的图象关于直线
的图象关于直线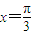 对称;
对称;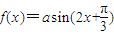 的图象可由g(x)=asin2x的图象向左平移
的图象可由g(x)=asin2x的图象向左平移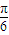 个单位而得到;
个单位而得到;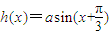 的图象上的所有点的纵坐标保持不变,横坐标缩短到原来的
的图象上的所有点的纵坐标保持不变,横坐标缩短到原来的 倍,可以得到函数
倍,可以得到函数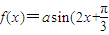 )的图象;
)的图象;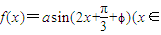 R)为偶函数,则
R)为偶函数,则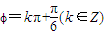 .
.