题目内容
设集合 ,分别从集合
,分别从集合 和
和 中随机取一个数
中随机取一个数 和
和 ,确定平面上的一个点
,确定平面上的一个点 ,记“点
,记“点 落在直线
落在直线 上”为事件
上”为事件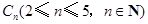 ,若事件
,若事件 的概率最大,则
的概率最大,则 的所有可能值为:
的所有可能值为:
| A.3 | B.4 | C.3和4 | D.2和5 |
C
解析试题分析:分别从集合A和B中随机取一个数a和b,组成一个有序数对,共有2×3中方法,要计算事件Cn的概率最大时n的所有可能值,要把题目中所有的情况进行分析求解,比较出n的所有可能值解:事件Cn的总事件数为6.只要求出当n=2,3,4,5时的基本事件个数即可.当n=2时,落在直线x+y=2上的点为(1,1);当n=3时,落在直线x+y=3上的点为(1,2)、(2,1);当n=4时,落在直线x+y=4上的点为(1,3)、(2,2);当n=5时,落在直线x+y=5上的点为(2,3);显然当n=3,4时,事件Cn的概率最大为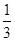 ,故选C
,故选C
考点:古典概型
点评:古典概型要求能够列举出所有事件和发生事件的个数,本题可以列举出所有事件,概率问题同其他的知识点结合在一起,实际上是以概率问题为载体,主要考查的是另一个知识点.

练习册系列答案
相关题目
已知随机变量X服从正态分布N(3,1),且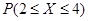 =0.6826,则
=0.6826,则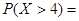 ( )
( )
| A.0.1585 | B.0.1588 | C.0.1587 | D.0.1586 |
已知一个样本的方差为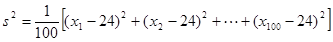 ,
,
若这个样本的容量为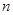 ,平均数为
,平均数为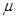 ,则
,则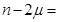 ( )
( )
| A.0 | B.24 | C.52 | D.148 |
若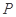 为
为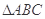 内一点,且
内一点,且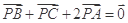 ,在
,在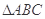 内随机撒一颗豆子,则此豆子落在
内随机撒一颗豆子,则此豆子落在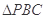 内的概率为( )
内的概率为( )
A.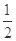 | B.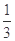 | C.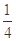 | D.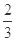 |
某人射击一次击中的概率为0.6,经过3次射击,此人恰有两次击中目标的概率为( )
A. | B. | C. | D.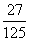 |
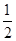 、
、 、
、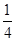 ,则有人能够解决这个问题的概率为
,则有人能够解决这个问题的概率为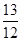
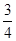
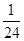
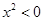 ”是不可能事件
”是不可能事件 服从的分布列如图,则随机变量
服从的分布列如图,则随机变量 等于 ( )
等于 ( )




 B.
B. C.
C.  D.
D. 
 (所以判断性别与运动有关,那么这种判断出错的可能性为( )(注:
(所以判断性别与运动有关,那么这种判断出错的可能性为( )(注: )
)


