题目内容
某学校为了研究学情,从高三年级中抽取了20名学生三次测试的数学成绩和物理成绩,计算出了他们三次成绩的平均名次如下表:| 学生序号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 数 学 | 1.3 | 12.3 | 25.7 | 36.7 | 50.3 | 67.7 | 49.0 | 52.0 | 40.0 | 34.3 |
| 物 理 | 2.3 | 9.7 | 31.0 | 22.3 | 40.0 | 58.0 | 39.0 | 60.7 | 63.3 | 42.7 |
| 学生序号 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| 数 学 | 78.3 | 50.0 | 65.7 | 66.3 | 68.0 | 95.0 | 90.7 | 87.7 | 103.7 | 86.7 |
| 物 理 | 49.7 | 46.7 | 83.3 | 59.7 | 50.0 | 101.3 | 76.7 | 86.0 | 99.7 | 99.0 |
(1)对名次优秀者赋分2,对名次不优秀者赋分1,从这20名学生中随机抽取2名,用ξ表示这两名学生数学科得分的和,求ξ的分布列和数学期望;
(2)根据这次抽查数据,是否在犯错误的概率不超过0.025的前提下认为物理成绩优秀与否和数学成绩优秀与否有关系?(下面的临界值表和公式可供参考:
| P(K2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
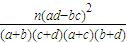 ,其中n=a+b+c+d)
,其中n=a+b+c+d)
【答案】分析:(1)根据条件ξ的取值为2,3,4,分别求出P(ξ=2),P(ξ=3),P(ξ=4).由此能求出ξ的分布列和数学期望Eξ.
(2)根据条件列出列联表,求出K2和P(K2≥5.024)=0.025,因此根据这次抽查数据在犯错误的概率不超过0.025的前提下,可以认为物理成绩优秀与否和数学成绩优秀与否有关系.
解答:解:(1)根据条件ξ的取值为2,3,4,
而且在20人中,数学成绩优秀的6人,不优秀的14人,所以有
P(ξ=2)=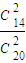 =
=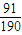 ,
,
P(ξ=3)=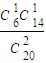 =
=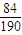 ,
,
P(ξ=4)=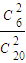 =
=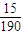 .
.
所以ξ的分布列为
(6分)
数学期望Eξ=2×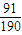 +3×
+3×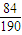 +4×
+4×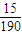 =2.6.(8分)
=2.6.(8分)
(2)根据条件列出列联表如下:
所以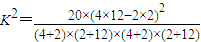 ≈5.4875>5.024.
≈5.4875>5.024.
又P(K2≥5.024)=0.025,
因此根据这次抽查数据在犯错误的概率不超过0.025的前提下,
可以认为物理成绩优秀与否和数学成绩优秀与否有关系.(12分)
点评:本小题主要考查统计与概率的相关知识,具体涉及到随机变量的分布列、数学期望的求法和统计案例中独立性检验等知识内容.
(2)根据条件列出列联表,求出K2和P(K2≥5.024)=0.025,因此根据这次抽查数据在犯错误的概率不超过0.025的前提下,可以认为物理成绩优秀与否和数学成绩优秀与否有关系.
解答:解:(1)根据条件ξ的取值为2,3,4,
而且在20人中,数学成绩优秀的6人,不优秀的14人,所以有
P(ξ=2)=
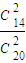 =
=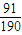 ,
,P(ξ=3)=
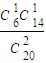 =
=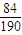 ,
,P(ξ=4)=
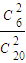 =
=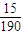 .
.所以ξ的分布列为
| ξ | 2 | 3 | 4 |
| P |  |  | 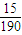 |
数学期望Eξ=2×
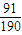 +3×
+3×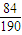 +4×
+4×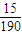 =2.6.(8分)
=2.6.(8分)(2)根据条件列出列联表如下:
| 物理优秀 | 物理不优秀 | 合计 | |
| 数学优秀 | 4 | 2 | 6 |
| 数学不优秀 | 2 | 12 | 14 |
| 合计 | 6 | 14 | 20 |
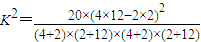 ≈5.4875>5.024.
≈5.4875>5.024.又P(K2≥5.024)=0.025,
因此根据这次抽查数据在犯错误的概率不超过0.025的前提下,
可以认为物理成绩优秀与否和数学成绩优秀与否有关系.(12分)
点评:本小题主要考查统计与概率的相关知识,具体涉及到随机变量的分布列、数学期望的求法和统计案例中独立性检验等知识内容.

练习册系列答案
相关题目
某学校为了研究学情,从高三年级中抽取了20名学生三次测试的数学成绩和物理成绩,计算出了他们三次成绩的平均名次如下表:
学校规定平均名次小于或等于40.0者为优秀,大于40.0者为不优秀.
(1)对名次优秀者赋分2,对名次不优秀者赋分1,从这20名学生中随机抽取2名,用ξ表示这两名学生数学科得分的和,求ξ的分布列和数学期望;
(2)根据这次抽查数据,是否在犯错误的概率不超过0.025的前提下认为物理成绩优秀与否和数学成绩优秀与否有关系?(下面的临界值表和公式可供参考:
K2=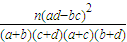 ,其中n=a+b+c+d)
,其中n=a+b+c+d)
| 学生序号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 数 学 | 1.3 | 12.3 | 25.7 | 36.7 | 50.3 | 67.7 | 49.0 | 52.0 | 40.0 | 34.3 |
| 物 理 | 2.3 | 9.7 | 31.0 | 22.3 | 40.0 | 58.0 | 39.0 | 60.7 | 63.3 | 42.7 |
| 学生序号 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| 数 学 | 78.3 | 50.0 | 65.7 | 66.3 | 68.0 | 95.0 | 90.7 | 87.7 | 103.7 | 86.7 |
| 物 理 | 49.7 | 46.7 | 83.3 | 59.7 | 50.0 | 101.3 | 76.7 | 86.0 | 99.7 | 99.0 |
(1)对名次优秀者赋分2,对名次不优秀者赋分1,从这20名学生中随机抽取2名,用ξ表示这两名学生数学科得分的和,求ξ的分布列和数学期望;
(2)根据这次抽查数据,是否在犯错误的概率不超过0.025的前提下认为物理成绩优秀与否和数学成绩优秀与否有关系?(下面的临界值表和公式可供参考:
| P(K2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
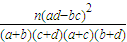 ,其中n=a+b+c+d)
,其中n=a+b+c+d)