Question

已知A、B、C是△ABC的三个内角，则在下列各结论中，不正确的为(　)

A．sin²A＝sin²B＋sin²C＋2sinBsinCcos(B＋C)

B．sin²B＝sin²A＋sin²C＋2sinAsinCcos(A＋C)

C．sin²C＝sin²A＋sin²B-2sinAsinBcosC

D．sin²(A＋B)＝sin²A＋sin²B-2sinBsinCcos(A＋B)

 

Answer 1

【答案】

D　

【解析】

试题分析：∵　sin²A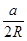＝()²，sin²B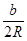＝()²，sin²C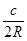＝()²

　　∴　四个选项分别可化为:a²＝b²＋c²-2bccosA

　　b²＝a²＋c²-2accosB

　　c²＝a²＋b²-2abcosC

　　c²＝a²＋b²＋2abcosC

　　显然c²＝a²＋b²＋2abcosC不对．故选D。

考点：本题主要考查正弦定理、余弦定理。

点评：简单题，主要看对正弦定理、余弦定理的理解记忆。