题目内容
数列{an}满足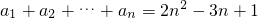
，则a4+a5+…+a10=________．
161
分析：在所给等式中分别取n=10，n=3，两式相减即可求得答案．
解答：由，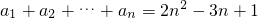
得a1+a2+…+a10=2×102-3×10+1①，
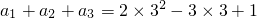②，
①-②得，a4+a5+…+a10=（2×102-3×10+1）-（2×32-3×3+1）=161，
故答案为：161．
点评：本题考查数列的求和问题，属基础题，正确理解数列前n项和的意义是解决问题的基础．
分析：在所给等式中分别取n=10，n=3，两式相减即可求得答案．
解答：由
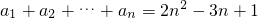，得a1+a2+…+a10=2×102-3×10+1①，
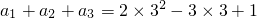②，①-②得，a4+a5+…+a10=（2×102-3×10+1）-（2×32-3×3+1）=161，
故答案为：161．
点评：本题考查数列的求和问题，属基础题，正确理解数列前n项和的意义是解决问题的基础．
练习册系列答案
英才点津系列答案
红果子三级测试卷系列答案
课堂练加测系列答案
相关题目
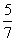若
,则a8等于( )
B.
C.
D.
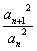N*),则称{an}为“等方比数列”.
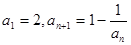，则a2007的值 （ ）
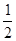D．2
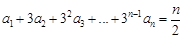，则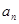
= ．
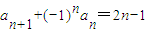，则{an}的前60项和为 ．