题目内容
“函数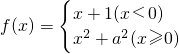 在点x=0处连续”是“a=1”的
在点x=0处连续”是“a=1”的
- A.充分不必要条件
- B.必要不充分条件
- C.充要条件
- D.既不充分也不必要条件
B
分析:由a=1可推出f(x)在x=1处连续,而f(x)在x=1处连续时推出a=1或a=-1,即可判断出两个命题的关系.
解答:f(x)在x=1处连续时,f(x)在x=1有定义且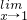 f(x)=
f(x)=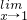 (2x+a2-2)=f(1)=1,
(2x+a2-2)=f(1)=1,
即a2=1,所以a=1或a=-1
a=1或a=-1?“a=1”是假命题
“a=1”?a=1或a=-1是真函数
所以函数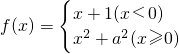 在点x=0处连续”是“a=1”的必要不充分条件.
在点x=0处连续”是“a=1”的必要不充分条件.
故选B.
点评:本题考查函数的连续性的概念,解题时要正确理解函数的连续性.要求学生掌握必要条件、充分条件以及充要条件的判断.
分析:由a=1可推出f(x)在x=1处连续,而f(x)在x=1处连续时推出a=1或a=-1,即可判断出两个命题的关系.
解答:f(x)在x=1处连续时,f(x)在x=1有定义且
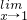 f(x)=
f(x)=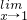 (2x+a2-2)=f(1)=1,
(2x+a2-2)=f(1)=1,即a2=1,所以a=1或a=-1
a=1或a=-1?“a=1”是假命题
“a=1”?a=1或a=-1是真函数
所以函数
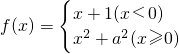 在点x=0处连续”是“a=1”的必要不充分条件.
在点x=0处连续”是“a=1”的必要不充分条件.故选B.
点评:本题考查函数的连续性的概念,解题时要正确理解函数的连续性.要求学生掌握必要条件、充分条件以及充要条件的判断.

练习册系列答案
相关题目
函数y=f(x)在x=x0处的导数f′(x0)的几何意义是( )
| A、在点x0处的斜率 | B、在点(x0,f(x0))处的切线与x轴所夹锐角的正切值 | C、在点(x0,f(x0))与点(0,0)连线的斜率 | D、曲线y=f(x)在点(xo,f(x0))处切线的斜率 |
 在
在 处的导数
处的导数 的几何意义是(
)
的几何意义是(
) 处的函数值
处的函数值  处的切线与x轴所夹锐角的正切值
处的切线与x轴所夹锐角的正切值