题目内容
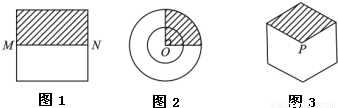
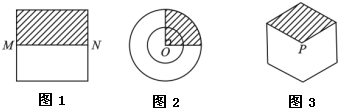
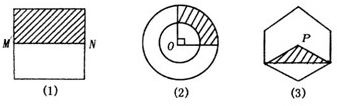
 形状如图所示的三个游戏盘中(图(1)是正方形,M、N分别是所在边中点,图(2)是半径分别为2和4的两个同心圆,O为圆心,图(3)是正六边形,点P为其中心)各有一个玻璃小球,依次摇动三个游戏盘后,将它们水平放置,就完成了一局游戏.
形状如图所示的三个游戏盘中(图(1)是正方形,M、N分别是所在边中点,图(2)是半径分别为2和4的两个同心圆,O为圆心,图(3)是正六边形,点P为其中心)各有一个玻璃小球,依次摇动三个游戏盘后,将它们水平放置,就完成了一局游戏.(I)一局游戏后,这三个盘中的小球都停在阴影部分的概率是多少?
(Ⅱ)用随机变量ζ表示一局游戏后,小球停在阴影部分的事件数与小球没有停在阴影部分的事件数之差的绝对值,求随机变量ζ的分布列及数学期望.
分析:(I)先根据几何概型的概率公式得到在三个图形中,小球停在阴影部分的概率,因为三个小球是否停在阴影部分相互之间没有关系,根据相互独立事件同时发生的概率得到结果.
(II)根据一次游戏结束小球停在阴影部分的事件数可能是0,1,2,3,得到ξ的可能取值是1,3,当变量等于3时,表示三个小球都在阴影部分或三个小球都不在阴影部分,这两种情况是互斥的,得到概率,分布列和期望.
(II)根据一次游戏结束小球停在阴影部分的事件数可能是0,1,2,3,得到ξ的可能取值是1,3,当变量等于3时,表示三个小球都在阴影部分或三个小球都不在阴影部分,这两种情况是互斥的,得到概率,分布列和期望.
解答:解:(I)“一局游戏后,这三个盘中的小球都停在阴影部分”分别记为事件A1、A2、A3,
由题意知,A1、A2、A3互相独立,
且P(A1)=
,P(A2)=
,P(A3)=
,…(3分)
∴P(A1 A2 A3)=P(A1) P(A2) P(A3)=
×
×
=
…(6分)
(II)一局游戏后,这三个盘中的小球都停在阴影部分的事件数可能是0,1,2,3,相应的小球没有停在阴影部分的事件数可能取值为3,2,1,0,所以ξ可能的取值为1,3,则
P(ξ=3)=P(A1 A2 A3)+P(
•
•
)=P(A1) P(A2) P(A3)+P(
)P(
)P(
)
=
×
×
+
×
×
=
,
P(ξ=1)=1-
=
. …(8分)
所以分布列为
…(10分)
数学期望Eξ=1×
+3×
=
. …(12分)
由题意知,A1、A2、A3互相独立,
且P(A1)=
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 3 |
∴P(A1 A2 A3)=P(A1) P(A2) P(A3)=
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 3 |
| 1 |
| 24 |
(II)一局游戏后,这三个盘中的小球都停在阴影部分的事件数可能是0,1,2,3,相应的小球没有停在阴影部分的事件数可能取值为3,2,1,0,所以ξ可能的取值为1,3,则
P(ξ=3)=P(A1 A2 A3)+P(
. |
| A1 |
. |
| A2 |
. |
| A3 |
. |
| A1 |
. |
| A2 |
. |
| A3 |
=
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 3 |
| 1 |
| 2 |
| 3 |
| 4 |
| 2 |
| 3 |
| 7 |
| 24 |
P(ξ=1)=1-
| 7 |
| 24 |
| 17 |
| 24 |
所以分布列为
| ξ | 1 | 3 | ||||
| P |
|
|
数学期望Eξ=1×
| 17 |
| 24 |
| 7 |
| 24 |
| 19 |
| 12 |
点评:本题考查几何概型的概率公式,考查相互独立事件同时发生的概率,考查离散型随机变量的分布列和期望,本题是一个典型的综合题目,可以作为高考卷中的题目出现.

练习册系列答案
 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案
相关题目
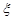 表示一局游戏后,小球停在阴影部分的事件数与小球没有停在阴影部分的事件数之差的绝对值,求随机变量
表示一局游戏后,小球停在阴影部分的事件数与小球没有停在阴影部分的事件数之差的绝对值,求随机变量