题目内容
已知椭圆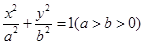 ,直线
,直线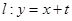 交椭圆于A、B两点,
交椭圆于A、B两点,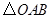 的面积为
的面积为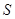 (
(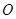 为原点),则函数
为原点),则函数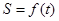 ( )
( )
A.是奇函数
B.是偶函数
C.不是奇函数,也不是偶函数
D.奇偶性与a、b有关
【答案】
B
【解析】
试题分析:由于a,b已知,只有t是变量,所以S一定是t的函数,即S=f(t),
f(-t)的意义是椭圆与直线y=x-t相交所得的三角形OA'B'的面积,
由于椭圆是关于原点的中心对称图形,直线y=x+t与直线y=x-t也关于原点中心对称,从图象上便可以看出三角形OAB与三角形OA'B'面积相等。
即f(t)=f(-t),所以S是偶函数,选B。
考点:本题主要考查椭圆的标准方程及几何性质,函数的奇偶性。
点评:创新题型,充分借助于椭圆的对称性,定性分析函数性质。

练习册系列答案
 一线名师提优试卷系列答案
一线名师提优试卷系列答案
相关题目
 已知椭圆C:
已知椭圆C: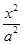 +
+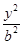 =1(a>b>0)的一个焦点是F(1,0),且离心率为
=1(a>b>0)的一个焦点是F(1,0),且离心率为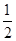 .
. +1,
+1,