题目内容
若复数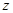 满足
满足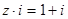 ,那么
,那么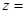
A.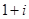 | B.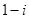 | C.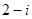 | D.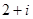 |
B
解析试题分析:结合复数对应相等可知,复数z满足z•i=1+i,∴两边同时乘以 ,得到
,得到 •z=i(1+i),∴z=-(i-1)=1-i.
•z=i(1+i),∴z=-(i-1)=1-i.
故选B.
考点:复数的运算
点评:解决的关键是通过变形表示为z,然后借助于复数的乘除法运算得到结论,属于基础题。

练习册系列答案
相关题目
已知 、
、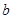 为实数,复数
为实数,复数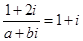 ,则
,则
A.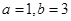 | B.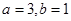 | C.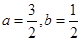 | D.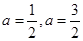 |
已知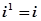 ,
,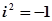 ,
, ,
,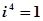 ,
,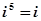 ,由此可猜想
,由此可猜想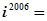 ( )
( )
A.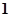 | B.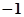 | C.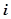 | D.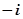 |
已知复数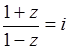 ,则
,则 的虚部为( )
的虚部为( )
| A.1 | B.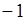 | C. | D.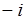 |
若复数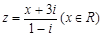 是实数,则
是实数,则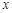 的值为( )
的值为( )
A.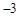 | B.3 | C.0 | D.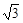 |
复数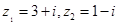 ,则复数
,则复数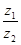 在复平面内对应的点位于 ( )
在复平面内对应的点位于 ( )
| A.第一象限 | B.第二象限 |
| C.第三象限 | D.第四象限 |
已知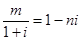 ,其中
,其中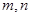 是实数,
是实数,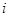 是虚数单位,则
是虚数单位,则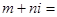 ( )
( )
A.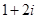 | B.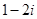 | C.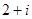 | D.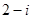 |
已知i为虚数单位,复数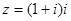 在复平面内对应的点位于( )
在复平面内对应的点位于( )
| A.第一象限 | B.第二象限 | C.第三象限 | D.第四象限 |
若复数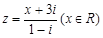 是实数,则
是实数,则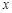 的值为
的值为
A.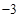 | B.3 | C.0 | D.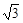 |