题目内容
在某次数学测试中,共有10 000人参加.为了分析该次测试成绩,工作人员从这10 000份试卷中随机地抽取100份进行分析,由于某种原因,数据遗失了,只有如图所示的频率分布直方图.
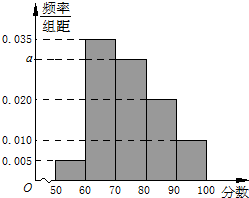
(1)试求直方图中a的值.
(2)若85分或85分以上为优秀生,试估计这次考试中优秀生的人数.

(1)试求直方图中a的值.
(2)若85分或85分以上为优秀生,试估计这次考试中优秀生的人数.
分析:(1)由频率分布直方图的性质可10(0.005+0.035+a+0.020×10+0.010)=1,解方程即可得到a的值;
(2)首先根据频率分布直方图可以求出成绩大于或等于85分的频率,然后利用频率可以估计出这10000名同学中这次考试中优秀生的人数.
(2)首先根据频率分布直方图可以求出成绩大于或等于85分的频率,然后利用频率可以估计出这10000名同学中这次考试中优秀生的人数.
解答:解:(1)由频率分布直方图的性质可得:
(0.005+0.035+a+0.020×10+0.010)×10=1
解得:a=0.030.
(2)数学成绩在[85,90)的频率为:0.1,
数学成绩在[90,100]的频率为:0.1.
所以数学成绩在[85,100]的人数为:10000(0.1+0.1)=2000.
估计这次考试中优秀生的人数为:2000人.
(0.005+0.035+a+0.020×10+0.010)×10=1
解得:a=0.030.
(2)数学成绩在[85,90)的频率为:0.1,
数学成绩在[90,100]的频率为:0.1.
所以数学成绩在[85,100]的人数为:10000(0.1+0.1)=2000.
估计这次考试中优秀生的人数为:2000人.
点评:本题考查读频率分布直方图的能力和利用统计图获取信息的能力,利用统计图获取信息时,必须认真观察、分析、研究统计图,才能作出正确的判断和解决问题.

练习册系列答案
相关题目