题目内容
如果有穷数列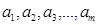 (
(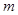 为正整数)满足
为正整数)满足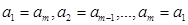 .即
.即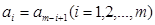 ,我们称其为“对称数列“例如,数列
,我们称其为“对称数列“例如,数列 ,
,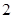 ,
,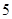 ,
,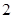 ,
, 与数列
与数列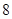 ,
,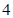 ,
,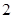 ,
,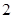 ,
,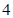 ,
, 都是“对称数列”.设
都是“对称数列”.设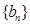 是项数为
是项数为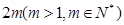 的“对称数列”,并使得
的“对称数列”,并使得 ,
,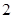 ,
,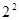 ,
,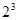 ,…,
,…,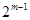 依次为该数列中连续的前
依次为该数列中连续的前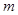 项,则数列
项,则数列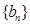 的前
的前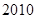 项和
项和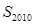 可以是
可以是
⑴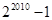 ⑵
⑵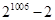 (3)
(3)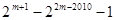
其中正确命题的个数为( )
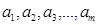 (
(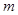 为正整数)满足
为正整数)满足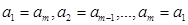 .即
.即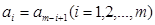 ,我们称其为“对称数列“例如,数列
,我们称其为“对称数列“例如,数列 ,
,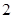 ,
,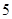 ,
,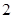 ,
, 与数列
与数列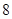 ,
,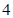 ,
,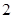 ,
,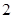 ,
,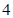 ,
,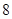 都是“对称数列”.设
都是“对称数列”.设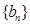 是项数为
是项数为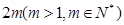 的“对称数列”,并使得
的“对称数列”,并使得 ,
,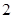 ,
,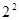 ,
,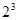 ,…,
,…,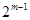 依次为该数列中连续的前
依次为该数列中连续的前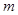 项,则数列
项,则数列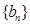 的前
的前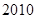 项和
项和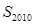 可以是
可以是⑴
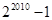 ⑵
⑵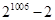 (3)
(3)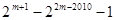
其中正确命题的个数为( )
| A.0 | B.1 | C.2 | D.3 |
C
专题:新定义.
分析:由题意由于新定义了对称数列,且已知数列bn是项数为不超过2m(m>1,m∈N*)的“对称数列”,并使得1,2,22,…,2m-1依次为该数列中前连续的m项,故数列bn的前2010项利用等比数列的前n项和定义直接可求(1)(2)的正确与否;对于(3),先从等比数列的求和公式求出任意2m项的和在利用减法的到需要的前201008项的和,即可判断.
解答:解:因为数列bn是项数为不超过2m(m>1,m∈N*)的“对称数列”,并使得1,2,22,…,2m-1依次为该数列中前连续的m项,故数列bn的前2010项可以是:①1,2,22,23…,21005,21005,…,22,1.
所以前2010项和S2010=2×
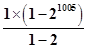 =2(21005-1),所以(1)错(2)对;
=2(21005-1),所以(1)错(2)对;对于 (3)1,2,22,…2m-2,2m-1,2 m-2,…,2,1,1,2,…2m-2,2m-1,2 m-2,…,2,1…m-1=2n+1,利用等比数列的求和公式可得:S2010=2m+1-22m-2010-1,故(3)正确.
故为C
点评:本题以新定义对称数列为切入点,运用的知识都是数列的基本知识:等差数列的通项及求和公式,等比数列的通项及求和公式,还体现了分类讨论在解题中的应用.

练习册系列答案
 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案
相关题目
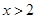 且
且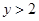 ”是“
”是“ ”的 ( )
”的 ( )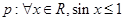 则
则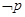 是
是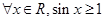
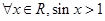
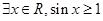

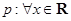 ,
,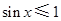 ,则(**** )
,则(**** )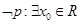 ,
,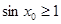
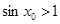
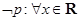 ,
,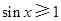
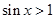
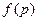 ,已知命题p:“若两条直线
,已知命题p:“若两条直线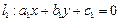 ,
,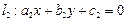 平行,则
平行,则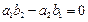 ”.那么
”.那么 ,则
,则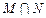 =" " ( )
=" " ( )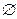
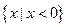
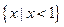

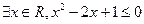 ”的否定是 。
”的否定是 。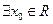 ,
,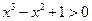 ”的否定是 ( )
”的否定是 ( ) 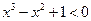
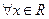 ,
,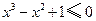
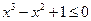
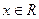 ,
,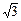 ,条件q:直线y=kx+2与圆x2+y2=1相切,则p是q的(
,条件q:直线y=kx+2与圆x2+y2=1相切,则p是q的(  )
) 件
件