题目内容
已知数列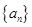 中,点
中,点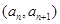
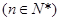 在直线
在直线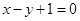 上,且
上,且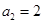 .
.
(Ⅰ)求证:数列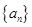 是等差数列,并求
是等差数列,并求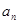 ;
;
(Ⅱ)设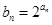 ,数列
,数列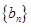 的前
的前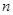 项和为
项和为 ,
,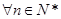 ,
,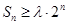 成立,求实数
成立,求实数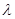 的取值范围.
的取值范围.
【答案】
(1)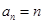 ;(2)
;(2)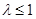 .
.
【解析】
试题分析:(1)将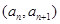 代入到直线
代入到直线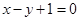 中,得到
中,得到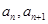 之间的关系,易知是等差数列,根据等差数列通项公式,求出最后的
之间的关系,易知是等差数列,根据等差数列通项公式,求出最后的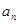 ;(2)利用(1)求出数列
;(2)利用(1)求出数列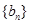 的前
的前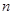 项和
项和 ,代入到
,代入到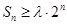 中,根据恒成立分离常数,求出最终
中,根据恒成立分离常数,求出最终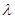 的取值范围.
的取值范围.
试题解析:(1)证明:由已知得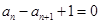 ,即
,即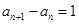
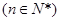
∴数列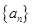 是等差数列,公差为
是等差数列,公差为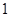 .
.
又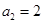 ,∴
,∴
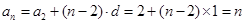
(2)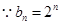 ,∴数列
,∴数列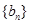 是等比数列,且首项为2,公比为2
是等比数列,且首项为2,公比为2
∴
由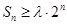 得
得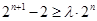 ,所以
,所以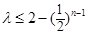
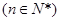
∴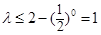 .
.
考点:等差数列通项公式的求法,等比数列的求和,恒成立问题.

练习册系列答案
相关题目
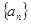 中,
中,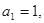 且点
且点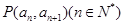 在直线
在直线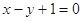 上。
上。 的通项公式;
的通项公式;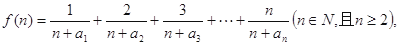 求函数
求函数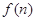 的最小值;
的最小值;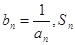 表示数列
表示数列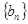 的前项和.试问:是否存在关于
的前项和.试问:是否存在关于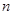 的整式
的整式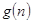 ,使得
,使得 对于一切不小于2的自然数
对于一切不小于2的自然数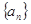 中,
中,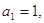 且点
且点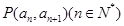 在直线
在直线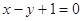 上。
上。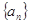 的通项公式;
的通项公式;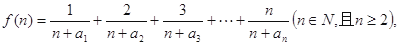 求函数
求函数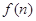 的最小值;
的最小值;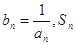 表示数列
表示数列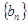 的前项和.试问:是否存在关于
的前项和.试问:是否存在关于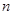 的整式
的整式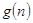 ,使得
,使得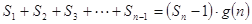 对于一切不小于2的自然数
对于一切不小于2的自然数 中,
中, ,点
,点 在直线y = x上,其中n = 1,2,3,….
在直线y = x上,其中n = 1,2,3,…. ,证明数列
,证明数列 是等比数列;
是等比数列;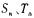 分别为数列
分别为数列 的前n项和,证明数列
的前n项和,证明数列 是等差数列
是等差数列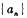 中,
中, ,点
,点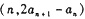 在直线y = x上,其中n = 1,2,3,….
在直线y = x上,其中n = 1,2,3,….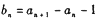 ,证明数列
,证明数列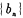 是等比数列;
是等比数列;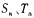 分别为数列
分别为数列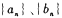 的前n项和,证明数列
的前n项和,证明数列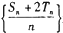 是等差数列
是等差数列