题目内容
若关于x的不等式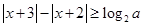
有解，则实数
的取值范围是： .
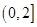
解析试题分析：∵关于
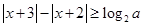的不等式有解，
表示数轴上的到
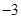和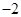
的距离之差，其最小值等于
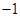，最大值是
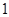，由题意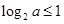
，∴
．
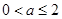考点：绝对值不等式的解法．
练习册系列答案
相关题目
题目内容
若关于x的不等式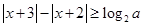有解，则实数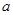的取值范围是： .
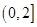
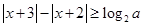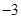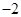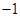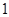解析试题分析：∵关于的不等式有解，表示数轴上的到和的距离之差，其最小值等于，最大值是，由题意，∴．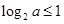
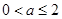考点：绝对值不等式的解法．
的解集为 
的解集为 .
的解集为 ____.
，
，（
、
）有唯一确定的
与之对应，称
、
的二元函数.现定义满足下列性质的二元函数
为关于实数
，当且仅当
时取等号；
；
对任意的实数z均成立.
；②
③
；④
.
使
成立，则实数
的取值范围是 
的解集是 ，
，则a=