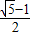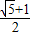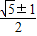题目内容
直角三角形三边成等比数列，公比为q，则q2的值为 ．
【答案】分析：设直角三角形的三边分别为：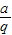
，a，aq（q≠1），再分别讨论当q＞1时与当q＜1时，进而结合勾股定理得到三边的关系，即可得到答案．
解答：解：设直角三角形的三边分别为：
，a，aq（q≠1），
当q＞1时，根据勾股定理可得：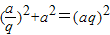
，即整理可得q4-q2-1=0，
解得：q2=
．
当q＜1时，根据勾股定理可得：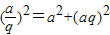
，即整理可得q4+q2-1=0，
解的：q2=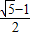
．
故答案为：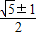
．
点评：本题主要考查等比数列的性质，三个数成等比数列时期设法为：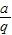
，a，aq，考查勾股定理的运用，以及分类讨论的数学思想．
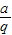，a，aq（q≠1），再分别讨论当q＞1时与当q＜1时，进而结合勾股定理得到三边的关系，即可得到答案．解答：解：设直角三角形的三边分别为：
，a，aq（q≠1），当q＞1时，根据勾股定理可得：
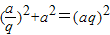，即整理可得q4-q2-1=0，解得：q2=
．当q＜1时，根据勾股定理可得：
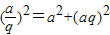，即整理可得q4+q2-1=0，解的：q2=
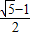．故答案为：
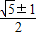．点评：本题主要考查等比数列的性质，三个数成等比数列时期设法为：
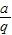，a，aq，考查勾股定理的运用，以及分类讨论的数学思想． 
练习册系列答案
同步练习河南大学出版社系列答案
同步练习西南大学出版社系列答案
相关题目
∶1
D.较小锐角的正弦为
