题目内容
从平面α上取6点,从平面β上取4点,这10个点最多可以确定多少个三棱锥?
分析:根据题意,由三棱锥的几何结构性质,分三种情况讨论:①从平面α上6个点中任取一个与平面β上4个点中任取3个构成三棱锥,②从平面α上6个点中任取2个与平面β上4个点中任取2个构成三棱锥,③从平面α上6个点中任取3个与平面β上4个点中任取1个构成三棱锥,由组合数公式计算每种情况的三棱锥数目,由分类计数原理计算可得答案.
解答:解:根据题意,分三种情况讨论:
①从平面α上6个点中任取一个与平面β上4个点中任取3个构成三棱锥,可以有
个,
②从平面α上6个点中任取2个与平面β上4个点中任取2个构成三棱锥,可以有
个,
③从平面α上6个点中任取3个与平面β上4个点中任取1个构成三棱锥,可以有
个,
根据加法原理最多有
+
+
=194个三棱锥.
①从平面α上6个点中任取一个与平面β上4个点中任取3个构成三棱锥,可以有
| C | 1 6 |
| C | 3 4 |
②从平面α上6个点中任取2个与平面β上4个点中任取2个构成三棱锥,可以有
| C | 2 6 |
| C | 2 4 |
③从平面α上6个点中任取3个与平面β上4个点中任取1个构成三棱锥,可以有
| C | 3 6 |
| C | 1 4 |
根据加法原理最多有
| C | 1 6 |
| C | 3 4 |
| C | 2 6 |
| C | 2 4 |
| C | 3 6 |
| C | 1 4 |
点评:本题考查排列、组合的应用,关键是结合立体几何的有关知识,确定分类讨论的标准.

练习册系列答案
相关题目
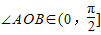 ”为事件C.
”为事件C.