题目内容
已知圆N:(x+2)2+y2=8和抛物线C:y2=2x,圆N的切线l与抛物线C交于不同的两点A,B.(I)当直线Z酌斜率为1时,求线段AB的长;
(II)设点M和点N关于直线y=x对称,问是否存在直线l,使得
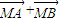 ?若存在,求出直线l的方程;若不存在,请说明理由.
?若存在,求出直线l的方程;若不存在,请说明理由.
【答案】分析:(1)由圆N:(x+2)2+y2=8,知圆心N为(-2,0),半径r=2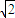 ,设A(x1,y1),B(x2,y2),设l的方程为y=x+m,由直线l是圆N的切线,知
,设A(x1,y1),B(x2,y2),设l的方程为y=x+m,由直线l是圆N的切线,知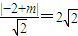 ,解得直线l的方程为y=x-2,由此能求出弦长|AB|.
,解得直线l的方程为y=x-2,由此能求出弦长|AB|.
(2)设直线l的方程为y=kx+m,由直线l是圆N的切线,得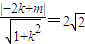 ,解得此时直线l的方程为y=-x+2;当直线l的斜率不存在时,l的方程为x=2
,解得此时直线l的方程为y=-x+2;当直线l的斜率不存在时,l的方程为x=2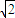 -2,则得
-2,则得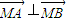 不成立.综上所述,存在满足条件的直线l,其方程为y=-x+2.
不成立.综上所述,存在满足条件的直线l,其方程为y=-x+2.
解答:解:(1)∵圆N:(x+2)2+y2=8,
∴圆心N为(-2,0),半径r=2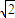 ,
,
设A(x1,y1),B(x2,y2),
当直线的斜率为1时,设l的方程为y=x+m,即x-y+m=0,
∵直线l是圆N的切线,∴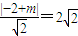 ,
,
解得m=-2,或m=6(舍去)
此时直线l的方程为y=x-2,
由 ,消去x得y2-2y-4=0,
,消去x得y2-2y-4=0,
∴△=(-2)2+16=20>0,
y1+y2=2,y1•y2=4,
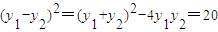 ,
,
∴弦长|AB|=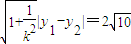 .
.
(2)(i)设直线l的方程为y=kx+m,即kx-y+m=0(k≠0),
∵直线l是圆N的切线,∴ ,
,
得m2-4k2-4mk-8=0,①
由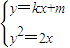 ,消去x得ky2-2y+2m=0,
,消去x得ky2-2y+2m=0,
∴△=4-4k×2m>0,即km< 且k≠0,
且k≠0,
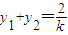 ,
,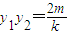 ,
,
∵点M与点N关于直线y=x对称,∴N(0,-2),
∴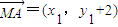 ,
,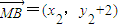 ,
,
∵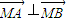 ,∴x1x2+(y1+2)(y2+2)=0,
,∴x1x2+(y1+2)(y2+2)=0,
将A,B在直线y=kx+m上代入并化简,得
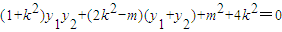 ,
,
代入 ,
,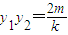 ,
,
得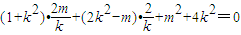 ,
,
化简,得m2+4k2+2mk+4k=0,②
①+②得2m2-2mk+4k-8=0,
即(m-2)(m-k+2)=0,
解得m=2,或m=k-2.
当m=2时,代入①,解得k=-1,满足条件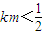 ,且k≠0,
,且k≠0,
此时直线l的方程为y=-x+2.
当m=k-2时,代入①整理,得7k2-4k+4=0,无解.
(ii)当直线l的斜率不存在时,
因为直线l是圆N的切线,所以l的方程为x=2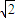 -2.
-2.
则得 ,y1+y2=0,
,y1+y2=0,
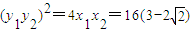 ,
,
即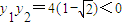 ,
,
由①得: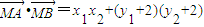
=x1x2+y1y2+2(y1+y2)+4
=20-12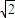 ≠0,
≠0,
当直线l的斜率不存在时,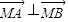 不成立.
不成立.
综上所述,存在满足条件的直线l,其方程为y=-x+2.
点评:本题考查线段长的求法,探索直线是否存在,具体涉及到圆的简单性质、抛物线的性质及其应用、直线与圆锥曲线的位置关系的应用.综合性强,难度大,是高考的重点.解题时要认真审题,仔细解答,注意合理地进行等价转化.
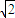 ,设A(x1,y1),B(x2,y2),设l的方程为y=x+m,由直线l是圆N的切线,知
,设A(x1,y1),B(x2,y2),设l的方程为y=x+m,由直线l是圆N的切线,知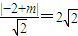 ,解得直线l的方程为y=x-2,由此能求出弦长|AB|.
,解得直线l的方程为y=x-2,由此能求出弦长|AB|.(2)设直线l的方程为y=kx+m,由直线l是圆N的切线,得
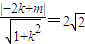 ,解得此时直线l的方程为y=-x+2;当直线l的斜率不存在时,l的方程为x=2
,解得此时直线l的方程为y=-x+2;当直线l的斜率不存在时,l的方程为x=2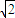 -2,则得
-2,则得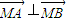 不成立.综上所述,存在满足条件的直线l,其方程为y=-x+2.
不成立.综上所述,存在满足条件的直线l,其方程为y=-x+2.解答:解:(1)∵圆N:(x+2)2+y2=8,
∴圆心N为(-2,0),半径r=2
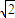 ,
,设A(x1,y1),B(x2,y2),
当直线的斜率为1时,设l的方程为y=x+m,即x-y+m=0,
∵直线l是圆N的切线,∴
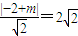 ,
,解得m=-2,或m=6(舍去)
此时直线l的方程为y=x-2,
由
 ,消去x得y2-2y-4=0,
,消去x得y2-2y-4=0,∴△=(-2)2+16=20>0,
y1+y2=2,y1•y2=4,
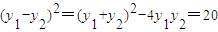 ,
,∴弦长|AB|=
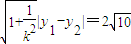 .
.(2)(i)设直线l的方程为y=kx+m,即kx-y+m=0(k≠0),
∵直线l是圆N的切线,∴
 ,
,得m2-4k2-4mk-8=0,①
由
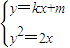 ,消去x得ky2-2y+2m=0,
,消去x得ky2-2y+2m=0,∴△=4-4k×2m>0,即km<
 且k≠0,
且k≠0,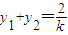 ,
,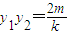 ,
,∵点M与点N关于直线y=x对称,∴N(0,-2),
∴
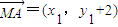 ,
,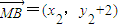 ,
,∵
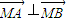 ,∴x1x2+(y1+2)(y2+2)=0,
,∴x1x2+(y1+2)(y2+2)=0,将A,B在直线y=kx+m上代入并化简,得
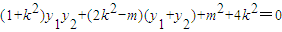 ,
,代入
 ,
,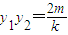 ,
,得
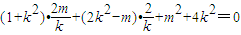 ,
,化简,得m2+4k2+2mk+4k=0,②
①+②得2m2-2mk+4k-8=0,
即(m-2)(m-k+2)=0,
解得m=2,或m=k-2.
当m=2时,代入①,解得k=-1,满足条件
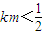 ,且k≠0,
,且k≠0,此时直线l的方程为y=-x+2.
当m=k-2时,代入①整理,得7k2-4k+4=0,无解.
(ii)当直线l的斜率不存在时,
因为直线l是圆N的切线,所以l的方程为x=2
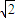 -2.
-2.则得
 ,y1+y2=0,
,y1+y2=0,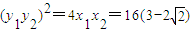 ,
,即
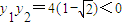 ,
,由①得:
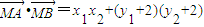
=x1x2+y1y2+2(y1+y2)+4
=20-12
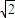 ≠0,
≠0,当直线l的斜率不存在时,
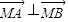 不成立.
不成立.综上所述,存在满足条件的直线l,其方程为y=-x+2.
点评:本题考查线段长的求法,探索直线是否存在,具体涉及到圆的简单性质、抛物线的性质及其应用、直线与圆锥曲线的位置关系的应用.综合性强,难度大,是高考的重点.解题时要认真审题,仔细解答,注意合理地进行等价转化.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
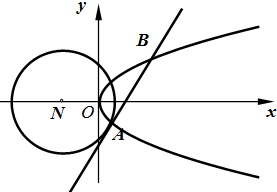 已知圆N:(x+2)2+y2=8和抛物线C:y2=2x,圆的切线l与抛物线C交于不同的两点A,B,
已知圆N:(x+2)2+y2=8和抛物线C:y2=2x,圆的切线l与抛物线C交于不同的两点A,B, (2012•烟台二模)已知圆N:(x+2)2+y2=8和抛物线C:y2=2x,圆N的切线l与抛物线C交于不同的两点A,B.
(2012•烟台二模)已知圆N:(x+2)2+y2=8和抛物线C:y2=2x,圆N的切线l与抛物线C交于不同的两点A,B.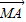 ⊥
⊥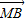 ,求出直线l的方程;若不存在,请说明理由.
,求出直线l的方程;若不存在,请说明理由.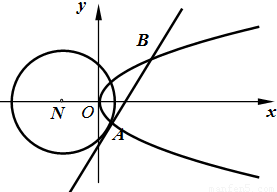
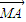 ⊥
⊥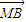 ,求出直线l的方程;若不存在,请说明理由.
,求出直线l的方程;若不存在,请说明理由.