题目内容
曲线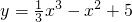 在x=1处的切线的斜率等于
在x=1处的切线的斜率等于
- A.

- B.

- C.1
- D.-1
D
分析:利用求导法则求出曲线方程的导函数,把x=1代入求出对应的导函数值即为所求切线方程的斜率.
解答:求导得:y′=x2-2x,
把x=1代入导函数得:y′|x=1=1-2=-1,
则曲线在x=1出切线的斜率为-1.
故选D
点评:此题考查了利用导数求曲线上过某点切线方程的斜率,要求学生掌握切点横坐标对应的导函数值即为切线方程的斜率,理解这点是解本题的关键.
分析:利用求导法则求出曲线方程的导函数,把x=1代入求出对应的导函数值即为所求切线方程的斜率.
解答:求导得:y′=x2-2x,
把x=1代入导函数得:y′|x=1=1-2=-1,
则曲线在x=1出切线的斜率为-1.
故选D
点评:此题考查了利用导数求曲线上过某点切线方程的斜率,要求学生掌握切点横坐标对应的导函数值即为切线方程的斜率,理解这点是解本题的关键.

练习册系列答案
 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案
相关题目
在平面直角坐标系中,由x轴的正半轴、y轴的正半轴、曲线y=ex以及该曲线在x=1处的切线所围成图形的面积是( )
| A、e | ||
| B、e-1 | ||
C、
| ||
D、
|
 在x=1处的切线方程为
( )
在x=1处的切线方程为
( ) B.
B.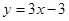 C.
C. D.
D.

 在x=1处的切线方程为
在x=1处的切线方程为 ,求实数a的值;
,求实数a的值; 的值域为
的值域为 ,求a的值;
,求a的值;