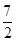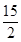题目内容
[2013·浙江高考]已知a,b,c∈R,函数f(x)=ax2+bx+c.若f(0)=f(4)>f(1),则( )
| A.a>0,4a+b=0 | B.a<0,4a+b=0 |
| C.a>0,2a+b=0 | D.a<0,2a+b=0 |
A
解析

练习册系列答案
相关题目
已知不等式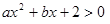 的解集为
的解集为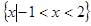 ,则不等式
,则不等式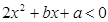 的解集为()
的解集为()
A.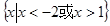 | B.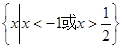 |
C.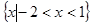 | D. |
若不等式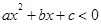 的解集为{x| x<-
的解集为{x| x<-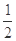 或x>
或x>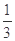 },则
},则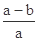 的值为 ( )
的值为 ( )
A.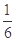 | B.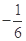 | C.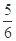 | D.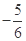 |
已知实数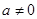 ,函数
,函数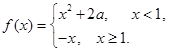 若
若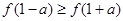 ,则实数
,则实数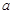 的取值范围是( )
的取值范围是( )
A.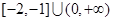 | B.[-2,-1] |
C.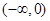 | D. |
对于实数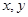 ,若
,若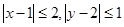 ,则
,则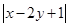 的最大值为( )
的最大值为( )
| A.4 | B.6 | C.8 | D.10 |
不等式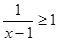 的解集为( )
的解集为( )
A.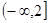 | B.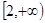 | C. | D. |
在R上定义运算“*”:x*y=x(1-y).若不等式(x-y)*(x+y)<1对一切实数x恒成立,则实数y的取值范围是( )
A.(-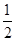 , ,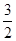 ) ) | B.(-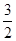 , ,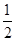 ) ) |
| C.(-1,1) | D.(0,2) |
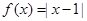 .
.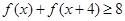 ;
;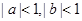 ,且
,且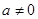 ,求证:
,求证: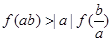 .
.