题目内容
将函数 的图象按向量
的图象按向量 平移后所得图象的函数解析式为( )
平移后所得图象的函数解析式为( )A.

B.

C.

D.

【答案】分析:先假设平移前、后的坐标,利用已知的平移向量,得出坐标之间的关系,再利用平移前的坐标满足的函数关系式,即可求得,平移后函数的解析式.
解答:解:设平移前的坐标为(a,b),平移后的坐标为(x,y),则
 =(x-a,y-b)
=(x-a,y-b)
∴a=x-1,b=y+1
∵
∴
∴
故选B.
点评:本题考查图象的变换,利用已知的平移向量,得出平移前、后的坐标之间的关系是解题的关键.
解答:解:设平移前的坐标为(a,b),平移后的坐标为(x,y),则
 =(x-a,y-b)
=(x-a,y-b)∴a=x-1,b=y+1
∵

∴

∴

故选B.
点评:本题考查图象的变换,利用已知的平移向量,得出平移前、后的坐标之间的关系是解题的关键.

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
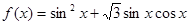

 的最小正周期和值域;
的最小正周期和值域; 的图象按向量
的图象按向量 平移后得到函数
平移后得到函数 的图
象,求函数
的图
象,求函数