题目内容
函数![]() 在x∈[1,4]上单调递减,则实数a的最小值为( )
在x∈[1,4]上单调递减,则实数a的最小值为( )
|
| A. | 1 | B. | 2 | C. | 4 | D. | 5 |
考点:
函数的单调性与导数的关系.
专题:
计算题;导数的概念及应用.
分析:
根据题意,函数f(x)的导数在区间[1,4]上恒小于或等于0.因此求出导数f'(x),列出相应不等式,解之即可得到实数a的最小值.
解答:
解:求得函数的导数f'(x)=1﹣![]() ,
,
∵函数![]() 在x∈[1,4]上单调递减,
在x∈[1,4]上单调递减,
∴f'(x)≤0即1﹣![]() ≤0,对任意的x∈[1,4]成立
≤0,对任意的x∈[1,4]成立
∴a≥2![]() 对任意的x∈[1,4]成立,得a≥4
对任意的x∈[1,4]成立,得a≥4
因此a的最小值是4
故选C
点评:
本题给出函数在指定区间上单调递减,求参数a的最小值,着重考查了函数求导数的法则和导数与单调性的关系等知识,属于基础题.

练习册系列答案
 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
相关题目
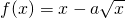 在x∈[1,4]上单调递减,则实数a的最小值为
在x∈[1,4]上单调递减,则实数a的最小值为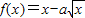 在x∈[1,4]上单调递减,则实数a的最小值为( )
在x∈[1,4]上单调递减,则实数a的最小值为( )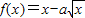 在x∈[1,4]上单调递减,则实数a的最小值为( )
在x∈[1,4]上单调递减,则实数a的最小值为( )