题目内容
(本题满分12分)
四个纪念币A、B、C、D,投掷时正面向上的概率如下表所示(0<a<1)
这四个纪念币同时投掷一次,设ξ表示出正面向上的个数。
(1)求概率p(ξ)
(2)求在概率p(ξ),p(ξ=2)为最大时,a的取值范围。
(3)求ξ的数学期望。
四个纪念币A、B、C、D,投掷时正面向上的概率如下表所示(0<a<1)
| 纪念币 | A | B | C | D |
| 概率 | 1/2 | 1/2 | a | a |
(1)求概率p(ξ)
(2)求在概率p(ξ),p(ξ=2)为最大时,a的取值范围。
(3)求ξ的数学期望。
a∈[ ] ,2a+1
] ,2a+1
 ] ,2a+1
] ,2a+1解:
(1)p(ξ个正面向上,4-ξ个背面向上的概率,其中ξ可能取值为0,1,2,3,4。
∴p(ξ="0)=" (1-
(1- )2
)2 (1-a)2=
(1-a)2= (1-a)2
(1-a)2
p(ξ="1)="
 (1-
(1- )
) (1-a)2+
(1-a)2+ (1-
(1- )2·
)2· a(1-a)=
a(1-a)=  (1-a)
(1-a)
p(ξ="2)=" (
( )2
)2 (1-a)2+
(1-a)2+
 (1-
(1- )
) a(1-a)+
a(1-a)+  (1-
(1- )2·
)2· a2=
a2= (1+2a-2 a2)
(1+2a-2 a2)
p(ξ="3)=" (
( )2
)2 a(1-a)+
a(1-a)+ 
 (1-
(1- )
) a2=
a2=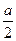
p(ξ="4)=" (
( )2
)2 a2=
a2= a2 ……………………………………5分
a2 ……………………………………5分
(2) ∵0<a<1,∴p(ξ="1)" <p(ξ=1),p(ξ="4)" <p(ξ=3)
则p(ξ="2)-" p(ξ="1)=" (1+2a-2 a2)-
(1+2a-2 a2)-  =-
=- ≥0
≥0
由
 ,即a∈[
,即a∈[ ] ……………………9分
] ……………………9分
(3)由(1)知ξ的数学期望为
Eξ=0× (1-a)2+1×
(1-a)2+1× (1-a)+2×
(1-a)+2× (1+2a-2a2)+3×
(1+2a-2a2)+3×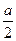 +4×
+4× =2a+1………………12分
=2a+1………………12分
(1)p(ξ个正面向上,4-ξ个背面向上的概率,其中ξ可能取值为0,1,2,3,4。
∴p(ξ="0)="
 (1-
(1- )2
)2 (1-a)2=
(1-a)2= (1-a)2
(1-a)2p(ξ="1)="

 (1-
(1- )
) (1-a)2+
(1-a)2+ (1-
(1- )2·
)2· a(1-a)=
a(1-a)=  (1-a)
(1-a) p(ξ="2)="
 (
( )2
)2 (1-a)2+
(1-a)2+
 (1-
(1- )
) a(1-a)+
a(1-a)+  (1-
(1- )2·
)2· a2=
a2= (1+2a-2 a2)
(1+2a-2 a2)p(ξ="3)="
 (
( )2
)2 a(1-a)+
a(1-a)+ 
 (1-
(1- )
) a2=
a2=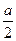
p(ξ="4)="
 (
( )2
)2 a2=
a2= a2 ……………………………………5分
a2 ……………………………………5分(2) ∵0<a<1,∴p(ξ="1)" <p(ξ=1),p(ξ="4)" <p(ξ=3)
则p(ξ="2)-" p(ξ="1)="
 (1+2a-2 a2)-
(1+2a-2 a2)-  =-
=- ≥0
≥0由

 ,即a∈[
,即a∈[ ] ……………………9分
] ……………………9分(3)由(1)知ξ的数学期望为
Eξ=0×
 (1-a)2+1×
(1-a)2+1× (1-a)+2×
(1-a)+2× (1+2a-2a2)+3×
(1+2a-2a2)+3×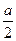 +4×
+4× =2a+1………………12分
=2a+1………………12分
练习册系列答案
 高中必刷题系列答案
高中必刷题系列答案
相关题目




 四个不同的赛场服务,每个赛场至少有一名志愿者。
四个不同的赛场服务,每个赛场至少有一名志愿者。 赛场服务的概率;
赛场服务的概率; 为这五名志愿者中参加
为这五名志愿者中参加 :“取出的2件产品中至多有1件是二等品”的概率
:“取出的2件产品中至多有1件是二等品”的概率 .
. ;
;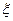 表示取出的2件产品中二等品的件数,求
表示取出的2件产品中二等品的件数,求