题目内容
13.已知函数f(x)=x2-2ax+2,当x∈[-1,+∞)时,f(x)≥0恒成立,求实数a的取值范围.分析 将二次函数进行配方,利用二次函数的图象和性质求解,要使不等式f(x)≥0恒成立,则只需求出函数在x∈[-1,+∞]时的最小值即可.
解答 解:∵f(x)=x2-2ax+2=(x-a)2+2-a2,
∴函数f(x)的对称轴是x=a,
①a≤-1时,f(x)min=f(-1)=2a+3,
∴只需2a+3≥0即可,
∴-$\frac{3}{2}$≤a≤-1,
②a>-1时,f(x)min=f(a)=2-a2,
∴只需2-a2≥0即可,
∴-1<a≤$\sqrt{2}$,
综上:-$\frac{3}{2}$≤a≤$\sqrt{2}$.
点评 本题主要考查二次函数的图象和性质,要注意分别讨论对称轴和区间之间的关系确定函数的最小值.

练习册系列答案
相关题目
4.设集合A={0,1},集合B={x|x>a},若A∩B=∅,则实数a的范围是( )
| A. | a≤1 | B. | a≥1 | C. | a≥0 | D. | a≤0 |



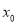 为函数
为函数 的零点,且满足
的零点,且满足 ,则这样的零点有( )
,则这样的零点有( ) 个 B.
个 B. 个
个 个 D.
个 D. 个
个