题目内容
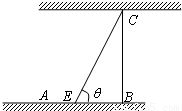
如图为河岸一段的示意图.一游泳者站在河岸的A点处,欲前往对岸的C点处,若河宽BC为100m,A、B相距100m,他希望尽快到达C,准备从A步行到E(E为河岸AB上的点),再从E游到C.已知此人步行速度为v,游泳速度为0.5v.(1)设∠BEC=θ,试将此人按上述路线从A到C所需时间T表示为θ的函数,并求自变量θ的取值范围;
(2)当θ为何值时,此人从A经E游到C所需时间T最小,其最小值是多少?
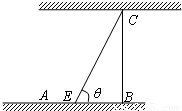
【答案】分析:(1)分别求出从A步行道E所用、从E游到C的路程,即可得到从A到C所需时间T表示为θ的函数,利用E位于A处时,θ取最小值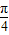 ,E位于B处时,θ取最大值
,E位于B处时,θ取最大值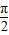 ,可得自变量θ的取值范围;
,可得自变量θ的取值范围;
(2)求导函数,可得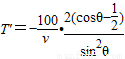 ,确定函数的单调性,即可得到θ=
,确定函数的单调性,即可得到θ=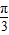 时,T取得极小值,也是最小值.
时,T取得极小值,也是最小值.
解答:解:(1)由题意,从A步行道E所用时间为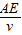 ,AE=AB-BE=100(1-
,AE=AB-BE=100(1-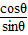 )
)
从E游到C,所用时间为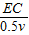 ,EC=
,EC=
∴T=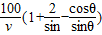
∵E位于A处时,θ取最小值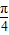 ,E位于B处时,θ取最大值
,E位于B处时,θ取最大值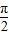
∴自变量θ的取值范围为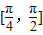 ;
;
(2)求导函数,可得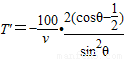
∴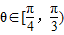 时,cosθ
时,cosθ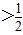 ,T′<0;
,T′<0;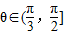 时,cosθ
时,cosθ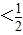 ,T′>0
,T′>0
∴θ=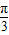 时,T取得极小值,也是最小值为
时,T取得极小值,也是最小值为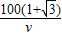 .
.
点评:本题考查函数模型的构建,考查利用导数解决实际问题,建模是关键.
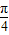 ,E位于B处时,θ取最大值
,E位于B处时,θ取最大值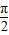 ,可得自变量θ的取值范围;
,可得自变量θ的取值范围;(2)求导函数,可得
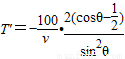 ,确定函数的单调性,即可得到θ=
,确定函数的单调性,即可得到θ=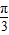 时,T取得极小值,也是最小值.
时,T取得极小值,也是最小值.解答:解:(1)由题意,从A步行道E所用时间为
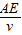 ,AE=AB-BE=100(1-
,AE=AB-BE=100(1-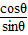 )
)从E游到C,所用时间为
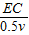 ,EC=
,EC=
∴T=
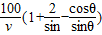
∵E位于A处时,θ取最小值
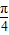 ,E位于B处时,θ取最大值
,E位于B处时,θ取最大值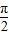
∴自变量θ的取值范围为
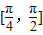 ;
;(2)求导函数,可得
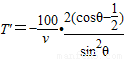
∴
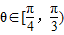 时,cosθ
时,cosθ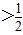 ,T′<0;
,T′<0;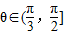 时,cosθ
时,cosθ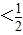 ,T′>0
,T′>0∴θ=
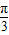 时,T取得极小值,也是最小值为
时,T取得极小值,也是最小值为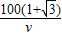 .
.点评:本题考查函数模型的构建,考查利用导数解决实际问题,建模是关键.

练习册系列答案
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案
相关题目
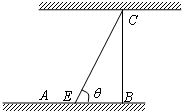 如图为河岸一段的示意图.一游泳者站在河岸的A点处,欲前往对岸的C点处,若河宽BC为100m,A、B相距100m,他希望尽快到达C,准备从A步行到E(E为河岸AB上的点),再从E游到C.已知此人步行速度为v,游泳速度为0.5v.
如图为河岸一段的示意图.一游泳者站在河岸的A点处,欲前往对岸的C点处,若河宽BC为100m,A、B相距100m,他希望尽快到达C,准备从A步行到E(E为河岸AB上的点),再从E游到C.已知此人步行速度为v,游泳速度为0.5v.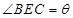 ,试将此人按上述路线从A到C所需时间T表示为
,试将此人按上述路线从A到C所需时间T表示为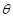 的函数;并求自变量
的函数;并求自变量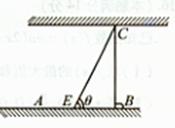
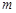 ,A、B相距100
,A、B相距100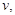 游泳速度为
游泳速度为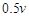 .
.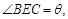 试将此人按上述路线从A到C所需时间T表示为
试将此人按上述路线从A到C所需时间T表示为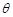 的函数,并求自变量
的函数,并求自变量