题目内容
集合 {
{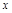 ,1},
,1},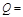 {
{ ,1,2},其中
,1,2},其中 {1, 2,…,9},则满足条件
{1, 2,…,9},则满足条件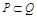 的事件的概率为( )
的事件的概率为( )
A. | B.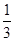 | C.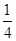 | D.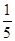 |
C
解析试题分析:根据题意,由于集合 {
{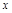 ,1},
,1},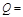 {
{ ,1,2},其中
,1,2},其中 {1, 2,…,9},那么可以对于x=2,y=3,4,5,….9,有7种,当x=3,y=3,只有1种,那么当x=4,…x=9都是一种,那么一共符合题意的有14种,列举法可知,按x有8种选择,y有7种选择,列表即可,共有56个,满足
{1, 2,…,9},那么可以对于x=2,y=3,4,5,….9,有7种,当x=3,y=3,只有1种,那么当x=4,…x=9都是一种,那么一共符合题意的有14种,列举法可知,按x有8种选择,y有7种选择,列表即可,共有56个,满足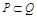 这样的点有14个,故根据古典概型的概率公式可知14:56=1:4,故概率为
这样的点有14个,故根据古典概型的概率公式可知14:56=1:4,故概率为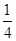 ,选C.
,选C.
考点:古典概型
点评:解决的关键是利用古典概型的概率公式来求解,属于基础题。

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
设 ,
, ,
, ,则
,则 = ( )
= ( )
A. | B.  | C. | D. |
若集合 ,
, ,则
,则 【 】.
【 】.
A. | B. | C. | D. |
已知集合 ,
,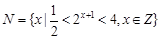 ,则
,则 ( )
( )
A. | B. | C. | D. |
设集合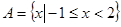 ,
,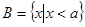 ,若
,若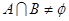 ,则
,则 的取值范围是( )
的取值范围是( )
A.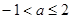 | B.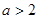 | C.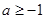 | D.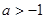 |
已知集合M={x ∈N | 8-x∈N},则M中元素的个数是( )。
| A.10 | B. 9 | C. 8 | D.无数个 |
设P={质数},Q={偶数},则P∩Q等于( )
| A.1?? | B.2 | C.{2} | D.N |
已知全集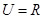 ,集合A=
,集合A=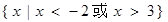 ,B=
,B=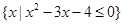 ,则集合
,则集合
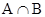 =
=
A.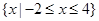 | B.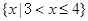 |
C. | D.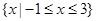 |
 ,
,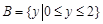 ,下列不表示从
,下列不表示从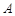 到
到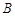 的映射的是( )
的映射的是( )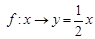 B.
B. 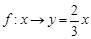
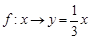 C.
C.